Chemical kinetics
- Details
- Written by: Jordi
- Category: Chemical kinetics
- Hits: 1123
The kinetics of chemical reactions is the part of chemistry that deals with the study of the speed with which reactions take place ( i ), one of the most important issues in any chemical process. Knowledge of reaction rates is important not only for its own sake, but also for the chemical industry, for understanding life-important biochemical processes, and in other fields of application. Therefore, we must define what is the speed with which a reaction takes place and learn to measure it, as well as discover what relationships exist between the speed of reactions and chemical equilibrium. But above all, we must know how the reactions take place and what are the microscopic processes that correspond to the changes in the chemical species. Since most reactions occur through molecular collisions of some kind, it is important to also study the nature of these collisions, and chemical kinetics is involved in that study.
i RSBerry, SARice and J.Ross - “Physical Chemistry - Part 3 – Physical and Chemical Kinetics”, 1st ed, 1980 – J.Wiley & Sons – (p. 1117).
- Details
- Written by: Jordi
- Category: Chemical kinetics
- Hits: 1452
Consider a chemical reaction of the generic type:
$$a\ A + b\ B \rightleftharpoons c\ C + d\ D$$
where $a$, $b$, $c$ and $d$ are the stoichiometric coefficients. Intuitively we could understand that there must be a concept such as reaction rate that is capable of measuring the speed with which a given reaction takes place. But, formally, how could we define the rate of reaction? For example, if we look at the reagent $A$, we can say that the reaction rate is the rate at which its total concentration in the medium decreases . In other words, the reaction rate would be the rate at which the reactant $A$ disappears, which is given by:
$$v_A = -\ \frac{d[A]}{dt}$$
But this form of definition presents a problem. Let us now consider the reaction product $C$. We could define the reaction rate in the same way as the speed with which the total concentration of $C$ increases in the medium, that is, as the amount:
$$v_C = \frac{d[C]}{dt}$$
And what is the problem? Well, for every $a$ moles of reactant $A$ that disappear in a given period of time, $c$ moles of product $C$ will have appeared. That is:
$$-\ \frac{1}{a}\ \cdot\ \frac{d[A]}{dt} = \frac{1}{c}\ \cdot\ \frac{d[C]}{dt }$$
- Details
- Written by: Jordi
- Category: Chemical kinetics
- Hits: 1263
Consider the case of a generic chemical reaction:
$$a\ A + b\ B\ \rightleftharpoons\ c\ C + d\ D$$
Of all the variables that affect the reaction rate, the most emphasis is usually placed on the concentrations of the substances that take part in the reaction. If variable such as temperature, pressure, and others are held constant, then it can be determined experimentally that the rate of a reaction is a simple function of those concentrations. Experimentally, it can be verified that, in most cases, the speed is directly proportional to the product of certain integer powers of the concentrations:
$$v = k\ \cdot\ [A]^{\alpha}\ \cdot\ [B]^{\beta}\ \cdot\ [C]^{\gamma}\ \cdot\ ...$$
- Details
- Written by: Jordi
- Category: Chemical kinetics
- Hits: 1208
In a first order reaction, the rate of reaction is directly proportional to the concentration of a single $A species and is independent of the concentrations of all others. Therefore, the reaction rate equation will be:
$$-\ \frac{d[A]}{dt} = k \cdot [A]$$
where k is the specific velocity coefficient. There are many reactions that follow this type of behavior. Among them are frequent decompositions and isomerizations.
To obtain the equation that allows us to know how the concentration of $A$ varies with time, we have to integrate the initial expression. We will have to separate variables first:
$$-\ \frac{d[A]}{dt} = k \cdot [A]\ \ \Rightarrow\ \ -\ \frac{d[A]}{[A]} = k \cdot dt$$
and now we integrate:
$$-\ \int_{[A]_0}^{[A]} \frac{d[A]}{[A]} = k \cdot \int_0^t dt$$
$$-\ \left ( {\ln [A] - \ln [A]_0} \right ) = k \cdot t$$
$$\ln {\frac{[A]}{[A]_0}} = -\ k \cdot t$$
$$[A] = [A]_0 \cdot e^{-\ k\cdot t}$$
where $[A]_0$ represents the concentration of the reactant $A$ at the start of the reaction, that is, when $t = 0$, and $[A]$ is the concentration of the same at any instant $t$.
The solution of the previous equation is done algebraically when we know the value of the specific speed constant. Otherwise, it can be done graphically by plotting $[A]/[A]_0$ as a function of time.
- Details
- Written by: Jordi
- Category: Chemical kinetics
- Hits: 1092
There are two main types of simple second-order reactions. The simplest form is one in which the reaction rate is proportional to the square of the concentration of a single species involved in the reaction. That is, when the velocity equation is of the form:
$$\displaystyle v = k \cdot [A]^2$$
The other possibility is that the reaction rate is proportional to the product of the concentrations of two species. I mean:
$$\displaystyle v = k \cdot [A] \cdot [B]$$
so that it is a first-order reaction with respect to each of the two species. We will analyze the two cases.
-
An example of the first type of second order reaction is the thermal decomposition of gaseous acetaldehyde (ethanal) which, at temperatures of the order of 500 ºC, decomposes into methane and carbon monoxide:
$$\displaystyle CH_{3}\!\!-\!CHO (g)\longrightarrow CH_4 (g) + CO (g)$$
For this reaction, it is known that:
$$\displaystyle v = k \cdot [CH_{3}\!\!-\!CHO]^2$$
The integration of this type of second order reactions is as follows.
Given the:
$$\displaystyle v = - \frac{d[A]}{dt} = k \cdot [A]^2$$
we separate variables:
$$\displaystyle - \frac{d[A]}{[A]^2} = k \cdot dt$$
and we integrate:
$$\displaystyle - \int_{[A]_0}^{[A]} \frac{d[A]}{[A]^2} = k \cdot \int_0^t dt \Rightarrow - \left. \left ( -\ \frac{1}{[A]}\right )\right|_{[A]_0}^{[A]} = k \cdot \left. (t)\right|_0^t$$
that is to say:
$$\displaystyle -\ \left [{\left (-\ \frac{1}{[A]}\right )\ -\ \left (-\ \frac{1}{[A]_0}\right ) }\right ] = k \cdot (t - 0)$$
so that we finally have:
$$\displaystyle \frac{1}{[A]} - \frac{1}{[A]_0} = k \cdot t$$
As can be seen, from the expression obtained, we see that the graphical representation of the inverse of the concentration of $A$ against time should give us a straight line with slope equal to $k$.
If we clear the concentration of $A$ we have:
$$\displaystyle [A] =\frac{1}{k \cdot t + \frac{1}{[A]_0}} = \frac{[A]_0}{[A]_0 \cdot k \cdot t+1}$$
so that plotting the concentration of $A$ against time will give us the hyperbolic curve:
- Details
- Written by: Jordi
- Category: Chemical kinetics
- Hits: 1267
A very useful concept in the study of the kinetics of a reaction is the half-life. This concept is used in many other fields. Perhaps the best known is the study of radioactive decay processes. These processes are, from our point of view, first order reactions, since the rate of disintegration of a radionuclide only depends on the amount of it present in the sample.
We will define the half-life of a reactant as the time required for half of its initial concentration to have reacted. It is usually represented as $t_{1/2}$.
In the case of a first order reaction, whose rate equation we know to be:
$$v = k \cdot [A]$$
Then, according to the definition of $t_{1/2}$, we have that:
$$t = t_{1/2} \Longrightarrow[A] = \frac{[A]_0}{2}$$
- Details
- Written by: Germán Fernández
- Category: Chemical kinetics
- Hits: 840
Let the competitive reactions be $A \stackrel{k_1}{\rightarrow}B$ and $A \stackrel{k_2}{\rightarrow}C$ of first order, we will determine $[A]$, $[B]$ and $[ C]$ as a function of time, assuming $[B]_0=[C]_0=0$. The variation of $[A]$ in time is given by the expression:
\begin{equation}\frac{d[A]}{dt}=-k_1[A]-k_2[A]\;\;\rightarrow \frac{d[A]}{dt}=(-k_1-k_2)[A]\end{equation}
Separating variables and integrating:
\begin{equation}[A]=[A]_0 e^{-( k_1+k_2)t} \label{ec1}\end{equation}
We now proceed to obtain the variation of $[B]$ with t
\begin{equation} \frac{d[B]}{dt}=k_1[A] \end{equation}
Substituting $[A]$ for $(\ref{ec1})$
- Details
- Written by: Germán Fernández
- Category: Chemical kinetics
- Hits: 1381
Let the consecutive reactions be $A \stackrel{k_1}{\rightarrow}B\stackrel{k_2}{\rightarrow}C$, of first order, we will determine $[A]$, $[B]$ and $[C]$ as a function of time, assuming $[B]_0 =[C]_0=0$. The variation of $[A]$ in time is given by the expression:
\begin{equation} \frac{d[A]}{dt}=-k_1[A]\label{ec101} \end{equation}
Separating variables and integrating:
\begin{equation} [A]=[A]_0 e^{-k_1 t}\label{ec102} \end{equation}
We now proceed to obtain the variation of $[B] $ with t
\begin{equation} \frac{d[B]}{dt}=k_1[A]-k_2[B] \end{equation}
Substituting $[A]$ for $(\ref{ec102} )$
\begin{equation} \frac{d[B]}{dt}=k_1[A]_0 e^{-k_1 t}-k_2[B] \end{equation}
This differential equation is of the form $\frac{dy}{dx}=f(x)+g(x)y$ and its solution is of the form $y=e^{w(x)}\left[\int e^{-w(x) }f(x)dx+c\right]$, where $w(x)=\int g(x)dx$.
- Details
- Written by: Germán Fernández
- Category: Chemical kinetics
- Hits: 1105
Obtain the kinetic equation for the radical linear chain reaction, $H_2 + Br_2 \rightarrow 2HBr$, which occurs through the following mechanism: \begin{eqnarray} Br_2 + M & \stackrel{k_i}{\rightarrow} & 2Br + M\label{ec110}\\ Br + H_2 & \stackrel{k_{p1}}{\rightarrow} & HBr + H\label{ec111}\\ H + Br_2 & \stackrel{k_{p2}}{\rightarrow} & HBr + Br\label{ec112}\\ H + HBr & \stackrel{k_{r}}{\rightarrow} & H_2 + Br\label{ec113}\\ 2Br + M & \stackrel{k_{t}}{\rightarrow} & Br_2 + M\label{ec114} \end{eqnarray}
$(\ref{ec110})$ Initiation stage
$(\ref{ec111})$ and $(\ref{ec112})$ Stages of propagation
$(\ref{ec113})$ Delay stage
$(\ref{ec114})$ Termination stage
We define the rate of the reaction for HBr: $r=\frac{1}{2}\frac{d[HBr]}{dt}$.
- Details
- Written by: Germán Fernández
- Category: Chemical kinetics
- Hits: 1175
For a reversible reaction $A\rightleftharpoons C$ of the first order, with kinetic constants for the forward reaction $k_1$ and reverse reaction $k{-1}$, we will determine $[A]$ and $[C]$ as a function of time , assuming that $[C]_0=0$. The variation of $[A]$ in time is given by the expression: \begin{equation}\label{1} \frac{d[A]}{dt}=-k_1[A]+k_{-1 }[C] \end{equation} From the stoichiometry we deduce, $[C]=[A]_0 -[A]$, substituting in $(\ref{1})$ \begin{equation} \frac{d[ A]}{dt}=-k_1[A]+k_{-1}\left([A]_0 - [A]\right) \end{equation}
- Details
- Written by: Germán Fernández
- Category: Chemical kinetics
- Hits: 1201
Enzymes are proteins with molecular weights of the order of 10 4 to 10 6 and catalyze most of the reactions that occur in living beings. The action of enzymes is very specific, catalyzing only a certain class of reactions. Furthermore, very small concentrations of enzyme are often sufficient to produce enormous catalytic activity on large amounts of substrate. The molecule on which the enzyme acts is called a substrate. The substrate binds to the active site of the enzyme, forming the enzyme-substrate complex. In this complex the substrate is transformed into the product, at which point it is released from the enzyme. There are many mechanisms to explain enzyme catalysis, here we will consider the simplest one, the Michaelis Menten mechanism, which is: \begin{equation} E+S\rightleftharpoons ES \rightarrow E+P \end{equation} Where E represents the enzyme , S the substrate, ES the enzyme-substrate complex and P the final product. The speed of the reaction will be given by the expression, $r=\frac{d[P]}{dt}=k_2[ES]$
- Details
- Written by: Germán Fernández
- Category: Chemical kinetics
- Hits: 1127
In ideal solutions, molarity [], mol/l is used as the unit of concentration. If the dissolution is real, it is necessary to use activities. It is only necessary to substitute the molar concentration for the activity in the equations.\\ Let the reaction be elementary, $aA+bB\rightleftharpoons cC+dD$, the speed of the direct reaction as a function of activities is given by the equation, $ r_d=k_da_{A}^{a}a_{B}^{b}$ and the rate of the reverse reaction by, $r_i=k_ia_{C}^{c}a_{D}^{d}$.
- Details
- Written by: Germán Fernández
- Category: Chemical kinetics
- Hits: 1326
Octave allows solving the equations of a kinetic system, in a very simple and efficient way. We will apply Octave to two complex kinetic systems: consecutive reactions and oscillating reactions (Lotka mechanism)
a) Consecutive reactions:
$A\stackrel{k_1}{\rightarrow} B \stackrel{k_2}{\rightarrow} C$, we solve the following differential equations with Octave: \begin{eqnarray} \frac{d[A]}{dt}& = & -k_1[A]\\ \frac{d[B]}{dt}& = & k_1[A]-k_2[B]\\ \frac{d[C]}{dt}& = & k_2[B ] \end{eqnarray}
We create a function that gives the velocity of the three components as a function of concentrations:
octave> function xdot = f(x,t) # x represents the concentrations of A, B and C, t is the time at a given instant and xdot are the derivatives of [A], [B] and [C] with respect to the time.
> global k # k is a vector representing the kinetic constants $k_1$ and $k_2$ is defined globally to be visible in the function above.
> xdot(1) = -k(1)*x(1) ; # define the first equation
> xdot(2) = k(1)*x(1) - k(2)*x(2); # define the second equation
> xdot(3) = k(2)*x(2); # define the third equation.
> end function
- Details
- Written by: Germán Fernández
- Category: Chemical kinetics
- Hits: 1885
For a first order reaction $aA \rightarrow P$, we write, \begin{equation} \frac{d[A]}{dt}=-k_A[A] \end{equation} This differential equation is very easy to solve , but suppose that we do not know its solution. Euler's method consists of approximating, for a small interval of time, the differentials by increments. \begin{equation} \frac{\Delta [A]}{\Delta t}=-k_A[A]\;\;\;\; \Rightarrow \Delta [A]=-k_A[A]\Delta t \end{equation} Substituting the increments for two concentrations close in time $[A]_n$ at time $t$ and $[A]_{n +1}$ to time $t_{n+1}$, gives us: \begin{equation} [A]_{n+1}-[A]_{n}=-k_A(t_{n+1} -t_n) \end{equation} This last equation represents the tangent line to the curve of [A] vs t at the point $[A]_n, t_n$.
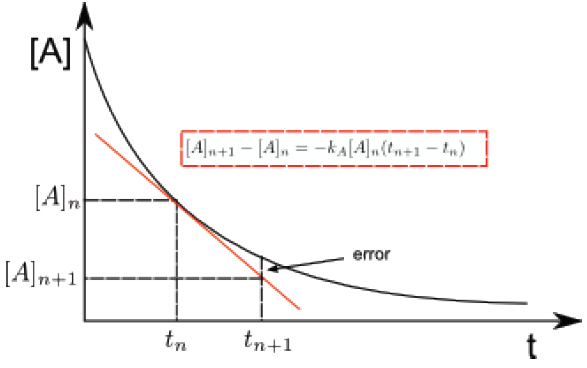
Let's see an example: Calculate [A] for t = 1s, if $[A]_0= 1\; mol/l$ and $k=10^{-3}s^{-1}$, we assume first-order kinetics. Applying equation (3). $[A] - 1 = -10^{-3}(1 - 0)$, therefore $[A] = (1-10^{-3})\; mol/l$
Read more: Numerical integration of kinetic data. Euler's method
- Details
- Written by: Germán Fernández
- Category: Chemical kinetics
- Hits: 1481
Arrhenius' Law is obtained from Van't Hoff's Law.
\begin{equation} \frac{dlnkº}{dT}=\frac{\Delta Hº}{RT^2} \end{equation}
Changing the enthalpy increase to the activation energy and the equilibrium constant to the kinetics, we obtain:
\begin{equation} \frac{dlnk}{dT}=\frac{E_a}{RT^2}\label{23} \end{equation}
Separating variables and integrating indefinitely
\begin{equation} \int dlnk=\int\frac{E_a}{RT^2}dT \;\rightarrow \; \; lnk=-\frac{Ea}{RT}+C \end{equation}
Calling the constant C lnA and solving for k yields: \begin{equation} k=Ae^{-E_a /RT} \end{equation}
- The pre-exponential factor, A, represents the frequency of collisions.
- $e^{-E_a /RT}$ represents the fraction of collisions that are reactive.
- Details
- Written by: Germán Fernández
- Category: Chemical kinetics
- Hits: 1199
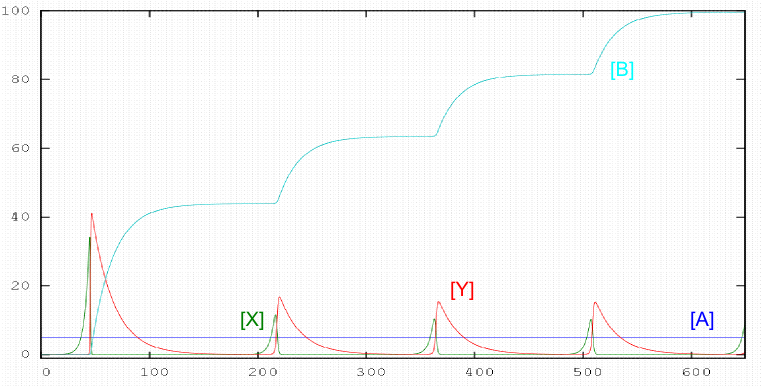
There are reactions in which the concentration of a reactant increases and decreases with time periodically. This type of behavior is associated with autocatalytic stages. In 1920 AJ Lotka proposed a simple mechanism in which the concentrations of components X and Y oscillate periodically. Lotka's mechanism is as follows:
\begin{equation} A+X\stackrel{k_1}{\rightarrow} 2X \end{equation} \begin{equation} X+Y\stackrel{k_2}{\rightarrow} 2Y \end{equation} \begin{equation} Y\stackrel{k_3}{\rightarrow} B \end{equation}
The oscillating behavior of this system is observed if the concentration of A is kept constant, therefore it is necessary to add A to the same rate that is spent.
- Details
- Written by: Germán Fernández
- Category: Chemical kinetics
- Hits: 1273
A very simple example of autocatalysis can be found in the following reaction: \begin{equation} A+B\stackrel{k}{\rightarrow}2B \;\; \Rightarrow r=-\frac{dA}{dt}=k[A][B] \end{equation} In the initial instants there is an increase in the concentration of B, which causes a rapid increase in velocity (note that B is reactant and product). However, as the reaction progresses, reagent A disappears and the speed begins to decrease, until it becomes zero, when this component disappears. The evolution of the concentrations of A and B over time is a sigmoid curve, which responds to the following equation: \begin{equation} kt=\frac{1}{[A]_0+[B]_0}ln\frac {[B]/[B]_0}{[A]/[A]_0} \end{equation}

- Details
- Written by: Germán Fernández
- Category: Chemical kinetics
- Hits: 1254
Rapid flow method
Many reactions are too fast to be studied by classical methods. Fast flow methods can be used for your study.
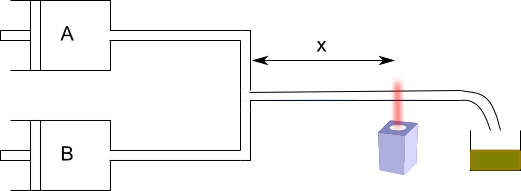
This system allows to measure [A] for small times. The fast flow method allows to study reactions with half-lives between 10 and 10 -3 seconds. The major limitation of fast flow techniques is the mixing time of the reagents. The most effective methods to determine these kinetics are the relaxation methods. In them, a reactive system in equilibrium is started, some variable is changed abruptly (T, P, ect.) and the return of the system to the new equilibrium is studied, being able to determine the kinetic constants.
- Details
- Written by: Germán Fernández
- Category: Chemical kinetics
- Hits: 1248
The rate of a reaction can strongly depend on the solvent. As an example, consider $S_N2$: $CH_3I + Cl^- \rightarrow CH_3Cl + I^-$, the speed depends on the solvent since this changes the value of k, due to the different solvation of the reactants. At other times, very fast reactions are limited by the rate of diffusion of the reactants through the solvent (solvent viscosity). The value of k also depends on hydrogen bonding. A reaction that can proceed through two competing mechanisms, rates can be affected and follow one mechanism in one solvent and the other in a different solvent.
Encounters, collisions, and the cell effect
In a gas the molecules are far apart and move freely. In a liquid, a molecule is surrounded by other molecules "solvent cell". This molecule crashes into the cell walls before being able to escape.
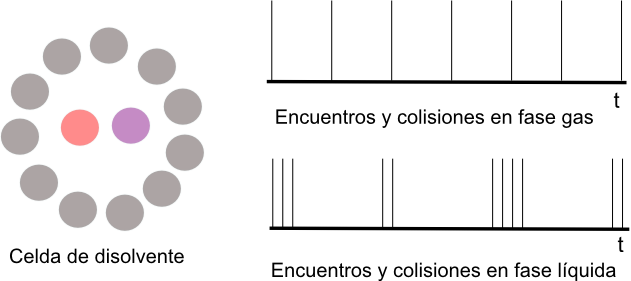
- Details
- Written by: Germán Fernández
- Category: Chemical kinetics
- Hits: 2102
The major steps of the $2H_2+O_2 \rightarrow H_2O$ reaction are believed to correspond to a branched chain reaction, with elementary steps: \begin{eqnarray} H_2 & \rightarrow & 2H\\ H_2+OH & \rightarrow & H + H_2O\\ H + O_2 & \rightarrow & OH + O\\ O + H_2 & \rightarrow & OH + H\\ 2H + wall & \rightarrow & H_2\\ H+O_2+M & \rightarrow & HO_2 + M^{\ast} \end{eqnarray} The $HO_2$ radical is long-lived, and the O and OH radicals are much more reactive than H.
1. Identify the stages of initiation, propagation, branching, and termination.
2. Show that, from the balance of the propagation and branching stages, the result is the overall reaction plus net radical generation.
3. Apply the steady state hypothesis to the concentrations of the free radicals O and OH to find their concentrations as a function of that of H (more abundant).
4. Considering that stage 5 is of order 1 (controlled by adsorption and diffusion on the walls) and stage 1 is of order zero (produced at a constant rate by external circumstances), find the differential equation that governs the generation of radicals h.
5. The solution of the differential equation has two regimes, depending on the sign of b. Discuss the conditions under which each of these regimes occurs, and their meaning.




