Second Principle | Thermodynamics
- Details
- Written by: Germán Fernández
- Category: Second principle of thermodynamics
- Hits: 1164
The second law of thermodynamics establishes the sense of spontaneous physical processes. It introduces a new magnitude called entropy that tends to increase its value in any irreversible thermodynamic process that takes place in an isolated system.
- Details
- Written by: Germán Fernández
- Category: Second principle of thermodynamics
- Hits: 1249
Kelvin-Planck statement , it is impossible for a system to carry out a cyclical process whose only effects are the flow of heat from a heat source to the system and the performance, by the system, of an equivalent amount of work.

- Details
- Written by: Germán Fernández
- Category: Second principle of thermodynamics
- Hits: 1217
A heat engine is a cyclically operating device that absorbs a quantity of heat from a hot source (for example, the boiler), does work -w on the surroundings, and releases a quantity of heat to a cold source.

The output or efficiency of a heat engine is the fraction of energy supplied that is converted into work. The machine consumes energy \(q_c\) per cycle and does work \(-w\), so the yield will be:
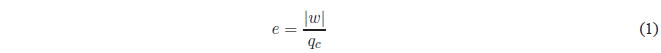
- Details
- Written by: Germán Fernández
- Category: Second principle of thermodynamics
- Hits: 1148
"No heat engine can be more efficient than a reversible heat engine, when both engines work between the same pair of temperatures." For the same amount of heat absorbed, the reversible engine generates the maximum amount of work.
- Details
- Written by: Germán Fernández
- Category: Second principle of thermodynamics
- Hits: 1171
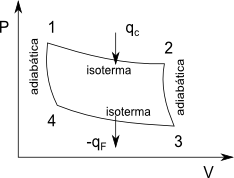
It is a reversible cycle that consists of two isothermal stages at different temperatures and two adiabatic stages. The working substance may not be an ideal gas, but in this development for simplicity we will use one mole of ideal gas.
- Details
- Written by: Germán Fernández
- Category: Second principle of thermodynamics
- Hits: 1236
Now let us calculate the performance of a Carnot cycle, using one mole of ideal gas as work substance and with only PV work.
We write the equation of the first law: \begin{equation} dU=dq+dw=dq-pdV \end{equation} For an ideal gas it is true that: \begin{equation} dU=C_vdT\;\;y\;\ ;P=\frac{nRT}{V} \end{equation} Substituting into the first law: \begin{equation} C_vdT=dq-\frac{nRT}{V}dV \end{equation} Dividing the entire equation by T \begin{equation} \frac{C_v}{T}dT=\frac{dq}{T}-nR\frac{dV}{V} \end{equation} Integrating over the Carnot cycle \begin{equation} \oint C_v\frac{dT}{T}=\oint\frac{dq}{T}-nR\oint\frac{dV}{V} \end{equation} The integrals $\oint C_v\frac{dT} {T}$ and $\oint\frac{dV}{V}$ are zero since the integrands are differentials of state functions and the integral over one cycle is zero.
- Details
- Written by: Germán Fernández
- Category: Second principle of thermodynamics
- Hits: 1238
Entropy is a state function discovered by Clausius in 1854 and defined by the following expression: \begin{equation} dS=\frac{dq}{T} \end{equation} The entropy change between two states 1 and 2 is obtained by integrating the differential expression: \begin{equation} \Delta S=\int_{1}^{2}\frac{dq}{T} \end{equation} Entropy is a measure of the disorder that a system possesses. The more disordered it is, the more entropy it has.
Thus, solid water (ordered molecules) has less entropy than liquid water (molecules with freedom of movement).
Entropy also tells us the direction that spontaneous processes follow. Suppose a container divided by a wall that contains nitrogen on one side and oxygen on the other, we remove the wall and the gases mix spontaneously. Nitrogen and oxygen molecules diffuse through every container, obtaining after a certain time a perfect mixture of both gases.
- Details
- Written by: Germán Fernández
- Category: Second principle of thermodynamics
- Hits: 1196
Cyclical process
The entropy change in a cyclic process is zero. The initial and final states coincide. \begin{equation}\Delta S=\oint\frac{dq}{T}=0\end{equation}
Reversible adiabatic process.
In an adiabatic process, no heat is exchanged between the system and the surroundings $dq_{rev}=0$ \begin{equation} \Delta S=\int\frac{dq_{rev}}{T}=0 \end{equation}
Reversible phase shift at constant T and P.
A phase change takes place at constant temperature and pressure. The temperature is outside the integral and the heat exchanged in the phase change is equal to the enthalpy change. \begin{equation} \Delta S=\int_{1}^{2}\frac{dq_{rev}}{T}=\frac{1}{T}\int_{1}^{2}dq_{rev }=\frac{q_{rev}}{T}=\frac{\Delta H}{T} \end{equation}
Read more: Calculation of entropy variations in some typical systems
- Details
- Written by: Germán Fernández
- Category: Second principle of thermodynamics
- Hits: 1122
In the previous sections we have considered the entropy changes in the system for the most typical processes. Now we will study the entropy variations that occur in the system and in the environment. We call universe the set of system plus environment that interacts with it. \begin{equation} \Delta S_{uni}=\Delta S_{sis}+\Delta S_{ent} \end{equation}
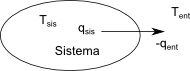
Let's calculate the change in entropy that the universe undergoes in a reversible process. Suppose there is an infinitesimal flow of heat dq from the system to the surroundings. For the process to be reversible, it is necessary that the temperature difference between the system and the surroundings be one dT, otherwise the process will be irreversible.
\begin{equation} dS_{uni}=dS_{sis}+dS_{in}=\frac{dq_{sis}}{T_{sis}}+\frac{dq_{in}}{T_{in}} \end{equation}
The heat received by the system is equal to the heat released by the surroundings, $q_{sis}=-q_{ent}$ and the temperatures only differ by an infinitesimal amount, $T_{sis}=T_{ent }$ , so we can consider them the same.
\begin{eqnarray} dS_{uni} & = & \frac{dq_{sis}}{T_{sis}}+\frac{-dq_{sis}}{T_{sis}}=0\\ \Delta S_{ uni} & = & 0 \end{eqnarray}
- Details
- Written by: Germán Fernández
- Category: Second principle of thermodynamics
- Hits: 1163
An isolated thermodynamic system reaches equilibrium when the entropy of the system is maximum. For example, the flow of heat from a hot body to a cold one implies an increase in entropy. This increase takes place until the bodies reach the same temperature (thermal equilibrium). The process of dissolving a salt in water involves an increase in entropy, which ceases when all the salt has dissolved.
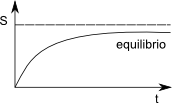
In an isolated system that is not in material equilibrium, spontaneous chemical reactions, or the transport of matter between phases are irreversible processes that increase entropy. These processes continue until the entropy reaches its maximum value.
The material equilibrium condition is the maximization of the entropy of the system plus that of the surroundings.
$\Delta S_{sis}+\Delta S_{in}$ maximum at equilibrium.
$\Delta S_{sis}$ is maximum at equilibrium for isolated systems.
- Details
- Written by: Jordi
- Category: Second principle of thermodynamics
- Hits: 1227
There is a way of understanding irreversible processes that has always amused me: suppose we put sand of two colors in a container. First we put the color 1 on the bottom. Then, on top, the color 2 is poured. Clearly, the sand is ordered, each color in its place. Now, we take a rod or a stick and we stir in a clockwise direction. After a certain time, all the sand will have been mixed and it will be impossible to distinguish the two colors: now only one more or less uniform color remains. If this mixing process were reversible, it would be enough to stir the sand with the stick again, this time turning it counterclockwise, and we could see how the colors separate again. It's not like that, is it? Well, this is an example of an irreversible process.
Another example, where we can see that processes in which entropy decreases, do so at the expense of energy consumption: Let's consider my office... Suppose (which is a lot to assume, but for the purposes of the example we'll pretend that were possible) that today everything is perfectly ordered. That is to say, each book in its place, magazines and papers properly placed in their trays or filing cabinets, collected computer cables, sharpened pencils and closed ballpoint pens placed in their cups... etc. OKAY? Well, as is easy to suppose, if we let time pass, the entropy will only increase constantly. That is to say, that the spontaneous process of habitual activity means that after a few days (even a few hours) all that is in a certain degree of disorder (to put it finely...). The process should not be confused with a reversible process. Of course, we can put everything back in its place, but it will be at the expense of expending large amounts of energy needed to put everything back in its place.



