Universitatis Chemia

Language Selector

Login Form

General Chemistry

Thermodynamics

Quantum Mechanic

Spectroscopy

Pysical Chemistry

¿Cuántos somos?

We have 301 guests and no members online

First Principle | Thermodynamics

Details
Category: First Law of thermodynamics
Hits: 153

In this section we will study a new state function, the internal energy U, and its relationship to heat and work.  Another important state function in chemistry is the enthalpy H.  will also be introduced  the heat capacities at constant pressure and volume, Cp and Cv, which give us the variations of internal energy and enthalpy with temperature.

Details
Category: First Law of thermodynamics
Hits: 217

As in classical mechanics, work is defined by the equation dw = F x dx,  where F x is the component of force F in the direction of motion and dx is the displacement. When F x and dx have the same sense, the work is positive, if they have  opposite directions the work is negative.

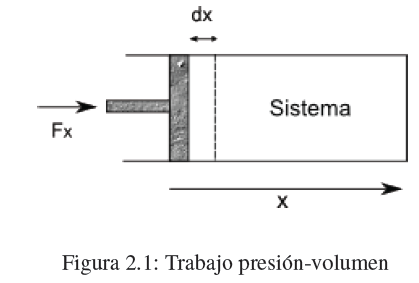
Consider a cylinder with a piston acted on by a force Fx producing a piston displacement dx.  The work done on the system is given by the equation, dw =F x dx.  Let A be the area of the piston, the pressure exerted by the piston on the system will be, P=F x /A, substituting in the work expression, dw = PAdx.

The product Adx represents the volume variation produced by the movement of the piston dV=-Adx.  Substituting in dw we get:

If we do work on the system (compression) dV<0 and the work is positive.  When the system does work on the surroundings (expansion) dV>0  work is negative.

Read more: Work Pressure-Volume (PV)

Details
Category: First Law of thermodynamics
Hits: 150

Heat is the second form of energy transfer that we are going to study. When two bodies at different temperatures come into contact through a thermally conductive wall, a flow of heat is produced from the hot body to the cold one until the temperatures are equal.



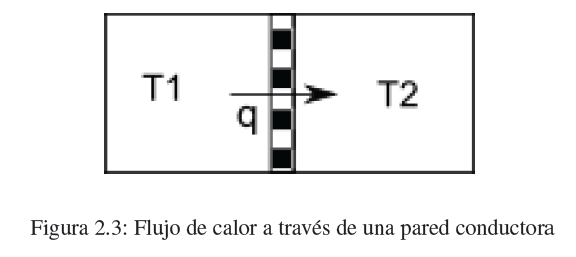
The amount of heat required to raise the temperature of the system by one dT is given by the expression:



where m is the mass of the system and c p its specific heat at constant pressure.

Read more: Heat in thermodynamics

Details
Category: First Law of thermodynamics
Hits: 177
What is internal energy? To understand the concept of internal energy, let's consider a gas. Each gas molecule has four types of energy:
Translational energy is kinetic energy due to the movement of the molecule.
Vibrational energy is the vibration energy of the atoms around the bond that unites them.
Rotational energy, due to the rotation of the molecule.
Electronic energy, produced by electronic transitions. It only matters at elevated temperatures.
The sum of these four types of energy gives us the total energy of a molecule. Adding the energy of all the molecules we will obtain the internal energy of the gas. Note that a monatomic gas has only translational and electronic energy since it cannot rotate or vibrate.

How can we change the internal energy of a system? The change of internal energy of a system is produced by exchanges of heat and/or work. When we do work or add heat to a system, we increase its internal energy. If the system loses heat or does work on the surroundings, its internal energy decreases.
The first law of thermodynamics can be written as follows:

Read more: First Law of Thermodynamics

Details
Category: First Law of thermodynamics
Hits: 162

The enthalpy H of a thermodynamic system is defined as:



The importance of this magnitude in chemistry lies in the fact that its variation coincides with the heat exchanged at constant pressure. It is very common for a chemical reaction to take place in an open vessel (at atmospheric pressure) and the heat exchanged will be an enthalpy change.

We start from the first law of thermodynamics: , the subscript p indicates constant pressure.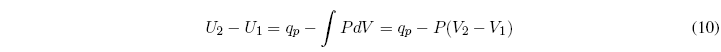



Clearing the heat and grouping terms we obtain: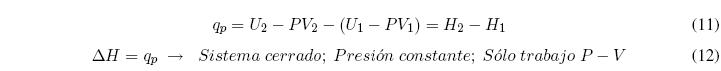

Read more: Enthalpy

Details
Category: First Law of thermodynamics
Hits: 148

The heat capacity of a closed system in an infinitesimal process is defined as the ratio between the heat exchanged and the temperature change produced.
For a process at P=cte, the heat capacity is given by the equation: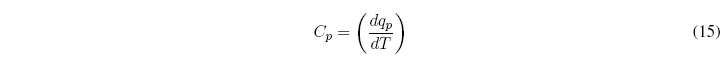



The heat capacity at constant volume is defined in the same way: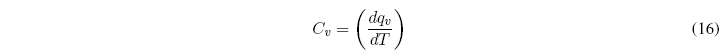



As , the above equations can be written as: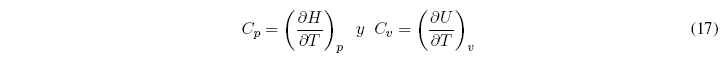



Therefore, C p and C v give us the variation of U and H with respect to temperature and must always take positive values.

We define molar heat capacities for pure substances as the ratio between C p and the number of moles of the substance.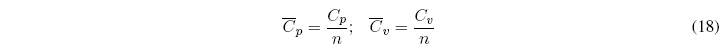

Read more: Heat capacity

Details
Category: First Law of thermodynamics
Hits: 145

An ideal gas satisfies the equation of state PV = nRT. The interactions between gas molecules are negligible, that is, there are no intermolecular forces. In an ideal gas, the change in volume does not affect the internal energy as long as the temperature is kept constant. A decrease in volume causes the molecules to be closer, but since there are no interactions between them, the internal energy does not change.

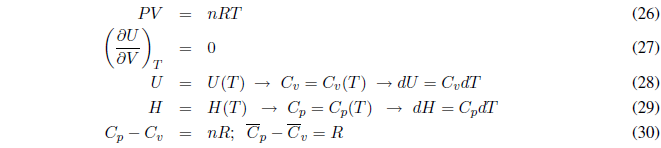
An ideal gas is defined as one that satisfies the following equations:
Next we consider some particular processes with ideal gases.

Details
Category: First Law of thermodynamics
Hits: 159

During this process the temperature is kept constant. Since the internal energy of ideal gases only depends on temperature: \(\Delta U=0\) and \(\Delta H=0\).

The first principle tells us: \(\Delta U=q+w\;\;\rightarrow q=-w\) . In this process, the heat exchanged is equal to the work done. We calculate the work done by the gas using the equation of state.
 
 
 
 
It can be put as a function of the initial and final state pressures using Boyle's law,
 
 
 
 
Substituting:
 
 

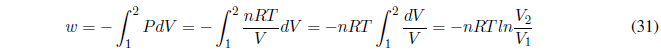
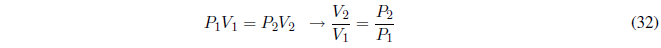
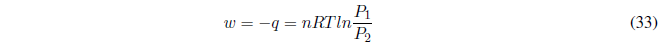
Details
Category: First Law of thermodynamics
Hits: 151

We start calculating the work, since P is constant it goes out of the integral.

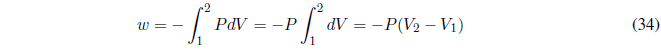
AP constant the heat exchanged is given by the enthalpy change.

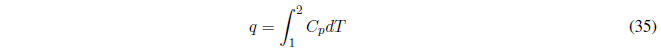
  • If \(C_p\) is independent of temperature it can be taken from the integral.
  • If we are given as data \(C_v\) instead of \(C_p\) remember the relationship between both magnitudes, \(C_p-C_v=R\).
  • The first principle gives us the internal energy change in the process, \(\Delta U =q+w\) .
  • The enthalpy change coincides with the heat exchanged.\(\Delta H =q\)

Details
Category: First Law of thermodynamics
Hits: 140

AV constant the work done is null \(w=0\).

Therefore, \(\Delta U=q\)
The heat is calculated with the relationship:
If the heat capacity is constant, the integral gives us:
The calculation of the enthalpy change is done with: \(\Delta H=\Delta U + V\Delta P\)

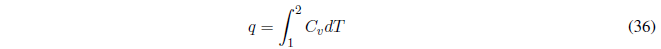
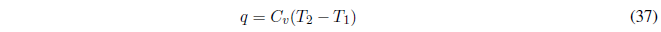
Details
Category: First Law of thermodynamics
Hits: 138

In an adiabatic process, the walls of the system prevent heat exchange, therefore, \(dq=0\;\;\rightarrow dU=dw\).

The internal energy variation can be calculated with:
if \(C_v\) remains constant,
The enthalpy change is calculated with:
Remember that in adiabatic processes the equations must be used:
where \(\gamma=\frac{C_p}{C_v}\)

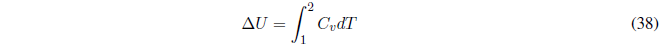
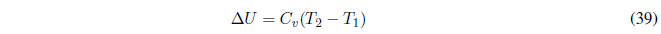
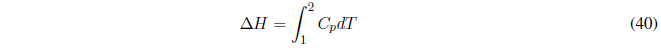
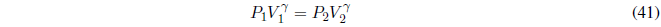
Details
Category: First Law of thermodynamics
Hits: 148

When a thermodynamic system goes from state 1 to state 2, it is said to have undergone a thermodynamic process. The intermediate thermodynamic states that lead from state 1 to 2 are called trajectories or paths. Two processes with different trajectories can connect the same initial and final states.

Let us now study some particular processes:
 
(a) Cyclic process , the initial and final states are the same. All state functions will be null for this process.
 
 
However, \(q\) and \(w\) do not have to be zero for a process of this type since they are not state functions and their value depends on the trajectory that the system follows to go from point 1 to 2. .
 
(b) Reversible phase change at constant T and P , the heat exchanged is the heat of phase change that can be measured experimentally. The work is calculated with the integral:
 
 

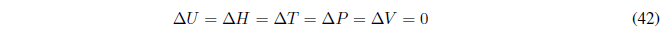
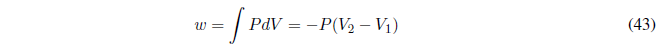
Read more: Calculation of q, w, U and H in thermodynamic processes