We start calculating the work, since P is constant it goes out of the integral.
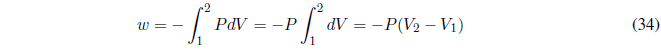
AP constant the heat exchanged is given by the enthalpy change.
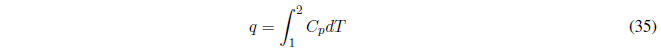
- If \(C_p\) is independent of temperature it can be taken from the integral.
- If we are given as data \(C_v\) instead of \(C_p\) remember the relationship between both magnitudes, \(C_p-C_v=R\).
- The first principle gives us the internal energy change in the process, \(\Delta U =q+w\) .
- The enthalpy change coincides with the heat exchanged.\(\Delta H =q\)



