Introduction to Thermodynamics
- Details
- Written by: Germán Fernández
- Category: Introduction to thermodynamics
- Hits: 1164
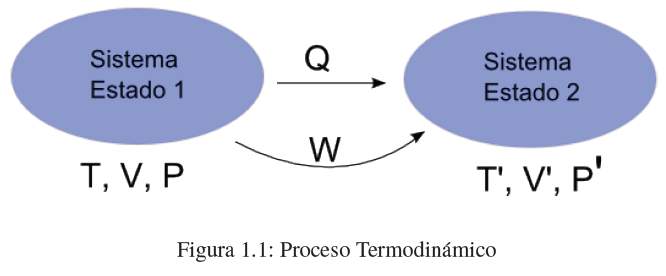
- Details
- Written by: Germán Fernández
- Category: Introduction to thermodynamics
- Hits: 1376
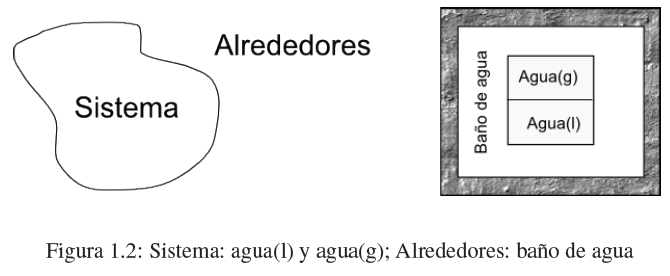
- Details
- Written by: Germán Fernández
- Category: Introduction to thermodynamics
- Hits: 2940
The walls of a system can be classified as: rigid or mobile , permeable or impermeable, conductive or adiabatic . The mobile walls are deformed allowing the change of the volume of the system. Pervious walls allow the passage of matter through the wall. The conductive walls allow the passage of heat, while the adiabatic ones do not (they are equivalent to the walls of a thermos).
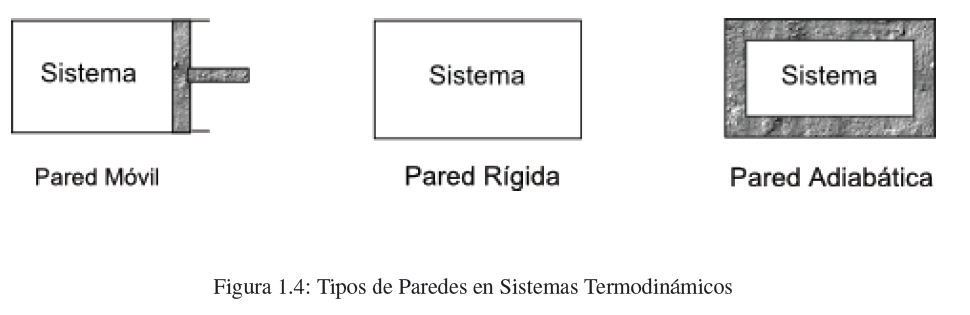
- Details
- Written by: Germán Fernández
- Category: Introduction to thermodynamics
- Hits: 1244
- Details
- Written by: Germán Fernández
- Category: Introduction to thermodynamics
- Hits: 1331
- Details
- Written by: Germán Fernández
- Category: Introduction to thermodynamics
- Hits: 1448
When a system is not homogeneous it consists of a series of parts with different properties called phases. An example of a heterogeneous system is the solution of NaCl in water that is in equilibrium with solid NaCl. This system has two phases, the aqueous and the solid.
- Details
- Written by: Germán Fernández
- Category: Introduction to thermodynamics
- Hits: 1140
- Details
- Written by: Germán Fernández
- Category: Introduction to thermodynamics
- Hits: 1150
- Details
- Written by: Germán Fernández
- Category: Introduction to thermodynamics
- Hits: 1159
- Details
- Written by: Germán Fernández
- Category: Introduction to thermodynamics
- Hits: 1236
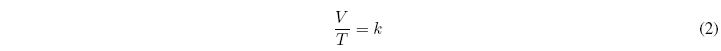
For a given mass of gas and constant pressure it is true that the ratio of the volume occupied by a gas and the temperature at which it is found is constant. This law gives fairly accurate results under low pressure conditions.
- Details
- Written by: Germán Fernández
- Category: Introduction to thermodynamics
- Hits: 1211
Boyle's law applies to processes that keep the gas mass and temperature constant, on the other hand, Charles' law keeps the gas mass and pressure constant. Let us now consider a process in which pressure, volume and temperature change. ![]()
We are going to divide the process into two stages, in the first the temperature is kept constant and in the second the pressure.
Let's apply Boyle's law to the first stage: ![]()
Now we will apply Charles's law to the second stage: 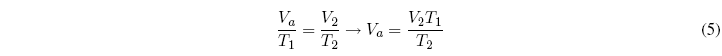
Equating both equations: 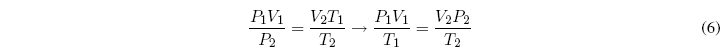
A m = constant, where m is the mass of the gas, it can be written: 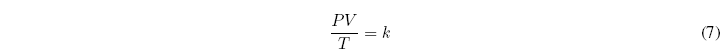
Let us now consider the variation of the mass, keeping the pressure and temperature of the gas constant, we arrive at the relationship: ![]() , since the mass is directly related to the number of moles, the previous equation can be written as:
, since the mass is directly related to the number of moles, the previous equation can be written as: ![]() , where n represents the number of moles of the gas.
, where n represents the number of moles of the gas.
The constant of proportionality k, is a universal constant, called the ideal gas constant and it is customary to represent it by R. Thus, the equation of state of ideal gases can be written as: ![]()
Where R = 0.082 atml/Kmol = 8.314 J/molK = 1.987 cal/molK
This law is only exact in the limit of zero pressure.
- Details
- Written by: Germán Fernández
- Category: Introduction to thermodynamics
- Hits: 1269
In 1810 Dalton established that the total pressure of a mixture of gases is equal to the sum of the pressures that each gas would exert if it were alone in the container.
Dalton's Law: "The sum of the partial pressures of each gas is equal to the total pressure of the gas mixture."
Let be a mixture of $n_1, n_2....$ moles of gases. The total pressure can be calculated with the equation: 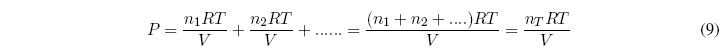
Another way of expressing Dalton's law, very useful in solving problems is: $P_i =x_iP$ , where $P_i$ is the partial pressure of gas i, $x_i$ is the mole fraction of gas i in the mixture of gases and P is the total pressure.
- Details
- Written by: Germán Fernández
- Category: Introduction to thermodynamics
- Hits: 1230
The relationship between the state variables of a system (P, V, T, n) is given by an equation called the equation of state.
As an example we have the ideal gas equation of state PV=nRT. Only an ideal gas fulfills this equation of state and, as can be seen, it relates the state variables, so that once three of them are known, the fourth can be obtained.
We can ask ourselves what happens with real gases, are there equations of state for them? The answer is yes, one of the best known equations applicable to real gases is the van der Waals equation which has the following form: 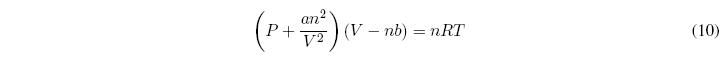
a and b are characteristic constants of each gas. If a and b are zero, the ideal gas equation is obtained. The term nb that subtracts from the volume takes into account the molecular repulsion. The term an 2 /V 2 takes into account the molecular attraction that tends to cause the pressure to be less than that predicted by the ideal gas equation.
There are six very useful partial derivatives in thermodynamics, because they can be measured very easily:
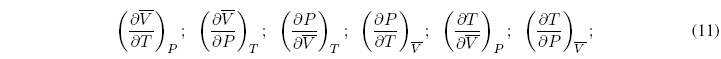
These six relations are not independent since three of them are the inverses of the other three.
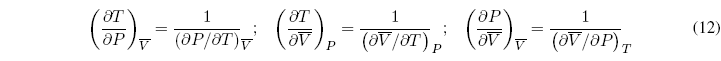
In addition, we can propose one more equation that relates three of the partial derivatives:
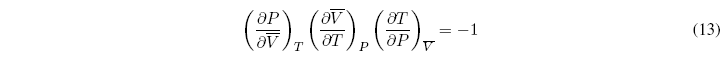
This relationship allows us to clear one of the relationships based on the other two. Therefore only two of the partial derivatives are independent and the remaining four can be calculated from them.
These independent derivatives are known as thermal expansion or coefficient of cubic expansion (\(\alpha\)) and isothermal compressibility (\(\kappa\)).
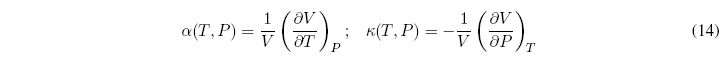
The relationship between both coefficients is given by the expression: 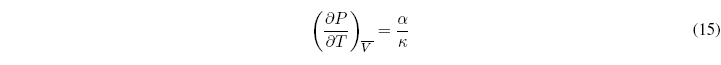
- Details
- Written by: Germán Fernández
- Category: Introduction to thermodynamics
- Hits: 1167
In thermodynamics it is necessary to use some mathematical tools such as the derivative. In this video I explain the definition of derivative and apply it to the function $y=x^2$. In the final part we define the partial derivative of a function.
- Details
- Written by: Germán Fernández
- Category: Introduction to thermodynamics
- Hits: 1206
In the following video, the derivative of a composite function is found by applying the chain rule. The total differential of a function of two variables is calculated and some useful relationships are obtained from it, such as the inverse derivative and the -1 rule.



