Equilibrium in one-component systems
- Details
- Written by: Germán Fernández
- Category: Phase equilibrium in one-component systems
- Hits: 1200
The phase rule attempts to answer the general question of how many independent variables are needed to define the equilibrium state of a multi-component phase system.
We define the number of degrees of freedom (f) of a system at equilibrium, as the number of independent intensive variables needed to specify its thermodynamic state.
Initially we will make two assumptions, which will later be removed:
- No chemical reaction occurs
- All chemical species are present in each of the phases.
Let be a system formed by c different chemical species and p phases.
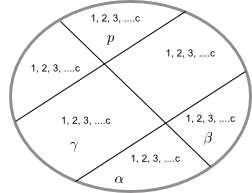
To give the composition of the system we need to specify the mole fractions of each component in each phase.
Phase composition $\alpha$: $x_{1}^{\alpha},x_{2}^{\alpha},x_{3}^{\alpha}, ........, x_ {c}^{\alpha}$
Composition of phase $\beta$: $x_{1}^{\beta},x_{2}^{\beta},x_{3}^{\beta}, ........, x_ {c}^{\beta}$
................................................................ ............................
Composition of phase $p$: $x_{1}^{p},x_{2}^{p},x_{3}^{p}, ........, x_{c}^ {p}$
So we need $c\times p$ mole fractions.
In addition, it is necessary to specify the temperature and pressure, which must be the same in all phases of the system, since the system is in thermodynamic equilibrium. That is, we have $c\times p +2$ variables.
- Details
- Written by: Germán Fernández
- Category: Phase equilibrium in one-component systems
- Hits: 1114
The enthalpy of fusion ($\Delta \bar{H}_{fus}$), is the heat required to convert one mole of solid to liquid.
Enthalpy of vaporization ($\Delta \bar{H}_{vap}$), is the heat required to change one mole of liquid to gas.
Enthalpy of sublimation ($\Delta \bar{H}_{sub}$), is the heat required to change one mole of solid to gas.
At the triple point the relation is fulfilled: $\Delta H_{sub}=\Delta H_{fus}+\Delta H_{ebu}$
- Details
- Written by: Germán Fernández
- Category: Phase equilibrium in one-component systems
- Hits: 1395
Clapeyron's equation allows us to calculate the slope of the equilibrium line $dP/dT$ at any value of P,T.
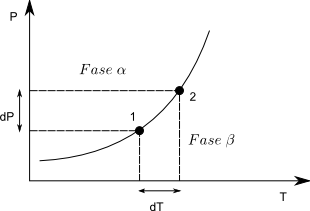
Let us consider two points on the equilibrium line, in any of them it must be fulfilled, $\mu^{\alpha}=\mu^{\beta}$, the subscript is unnecessary because it is a pure substance. As the chemical potential coincides with the Gibbs free energy molar $\bar{G}_{1}^{\alpha}=\bar{G}_{1}^{\beta}$. Going from point (1) to (2) produces an infinitesimal change in G and we can write:
- Details
- Written by: Germán Fernández
- Category: Phase equilibrium in one-component systems
- Hits: 1227
Let us consider a system with only one component $(H_2O)$, we neglect the dissociation. We are going to represent any state of the system by means of a phase diagram.
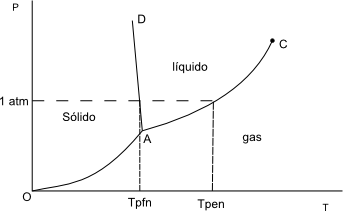
At low temperatures and moderate or high pressures we have the solid phase. At low pressures the gas phase and at intermediate temperatures and pressures the liquid phase.



