Rotation vibration in diatomic
- Details
- Written by: Germán Fernández
- Category: Rotation vibration in diatomic molecules
- Hits: 1199
The Born-Oppenheimer approximation makes it possible to separate the Schrodinger equation for a molecule into an electronic and a nuclear equation. The Schrödinger equation for nuclear motion in a given electronic state is given by:
\begin{equation}\label{1} \left(\hat{T}_N + E_e\right)\psi_N=E\psi_N \end{equation}
Where $\hat{T}_N$ represents the kinetic energy of the nuclei. $E_e$ is the nuclear potential (electronic energy and repulsion between nuclei) and depends on the electronic state of the molecule. E is the total energy of the molecule.
Particularizing these results for a diatomic molecule composed of two atoms 1 and 2 of masses $m_1$ and $m_2$
\begin{equation}\label{2} \left[-\frac{\hbar^2}{2m_1}\nabla_{1}^{2}-\frac{\hbar^2}{2m_2}\nabla_{2 }^{2} +E_e(R)\right]\psi_N =E\psi_N \end{equation}
- Details
- Written by: Germán Fernández
- Category: Rotation vibration in diatomic molecules
- Hits: 1186
The kinetic energy of the internal movement can be separated into two energies, it can be divided into rotational kinetic energy and vibrational kinetic energy. Initially we will make the approximation that both movements are independent, since the rotational movement depends on the angles $\theta$ and $\varphi$ while the vibrational movement only depends on the distance between nuclei $R$.
\begin{equation} \frac{-\hbar}{2\mu}\nabla^2\psi_{rot}=E_{rot}\psi_{rot} \end{equation}
The rigid rotor model gives us the rotational energy of a diatomic molecule:
\begin{equation}\label{4} E_{rot}=\frac{\hbar^2 J(J+1)}{2I_e} \end{equation}
Where $I_e=\mu R_{e}^{2}$ is the equilibrium moment of inertia.
We can also write the rotational energy in terms of the rotational constant $B_e$, where $B_e=\frac{h}{8\pi^2I_e}$
\begin{equation}\label{5} E_{rot}=B_e hJ(J+1) \end{equation}
The rotation quantum number $J$ takes values: 0,1,2,3..... and the rotational levels are $(2J+1)$ times degenerate.
- Details
- Written by: Germán Fernández
- Category: Rotation vibration in diatomic molecules
- Hits: 1410
The vibrational energy is obtained by solving the vibrational Schrödinger equation
\begin{equation}\label{6} \left[-\frac{\hbar^2}{2\mu}\frac{d^2}{dR^2}+E_e(R)\right]\psi_{ vib}(R)=(E_{vib}+E_{ele})\psi_{vib}(R) \end{equation}
The Taylor series expansion of the potential energy $E_e(R)$ around the equilibrium distance $R_e$ gives us:
\begin{equation}\label{71} E_e(R)\approx E_e(R_e)+\frac{1}{2}\frac{d^2E_e(R_e)}{dR^2}(R-R_e)^ 2+..... \end{equation}
The quantity $E_e(R_e)=E_{el}$ is constant for a given electronic state and is called equilibrium electronic energy.
- Details
- Written by: Germán Fernández
- Category: Rotation vibration in diatomic molecules
- Hits: 1168
The energy obtained for the harmonic oscillator depends on the development ( ecuación 2 ) that is truncated by the second term. Adding the third and fourth derivatives to the expansion gives a better approximation for the energy. The correction term for the vibrational energy equation is: $-h\nu_e x_e(v+\frac{1}{2})^2$, where $\nu_e x_e$ is known as the anharmonicity constant. The corrected vibrational energy is: $ E_{vib}=(v+\frac{1}{2})h\nu_e-h\nu_e x_e(v+\frac{1}{2})^2$
The inclusion of anharmonicity leaves us the internal energy of the molecule as follows:
\begin{equation}\label{13} E_{int}=B_e h J(J+1)+(v+\frac{1}{2})h\nu_e-h\nu_e x_e(v+\frac{1} {2})^2+E_{ele} \end{equation}
- Details
- Written by: Germán Fernández
- Category: Rotation vibration in diatomic molecules
- Hits: 1424
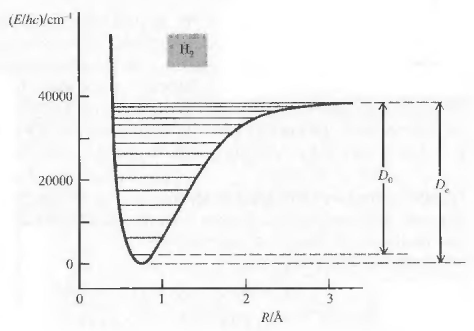
In the ground state the rotational energy is zero $(J=0, E_{rot}=0)$. However, the vibrational energy in the ground state of the molecule is not zero, with v=0 $E_{vib}=\frac{1}{2}h\nu_e -\frac{1}{4}h\nu_e x_e$. Note that the anharmonicity correction has been included.
Calling $D_0$ the dissociation energy of the fundamental vibrational state and $D_e$ equilibrium dissociation energy, the following relation between the two can be written:
\begin{equation} D_e=D_0+\frac{1}{2}h\nu_e-\frac{1}{4}h\nu_ex_e \end{equation}
- Details
- Written by: Germán Fernández
- Category: Rotation vibration in diatomic molecules
- Hits: 1105
As the vibrational quantum number increases, the vibrational energy of the molecule increases as well as the average distance between the nuclei. The increase in $R_{meas}$ produces an increase in the moment of inertia $I=\mu R_{meas}^{2}$. Rotational energy decreases as it is inversely proportional to the moment of inertia. To consider this effect, the term $-h\alpha_e(v+1/2)J(J+1)$ is added to the energy, where $\alpha_e$ is the rotation-vibration coupling constant.
- Details
- Written by: Germán Fernández
- Category: Rotation vibration in diatomic molecules
- Hits: 1383
As the rotational energy increases, the internuclear distance increases, due to the centrifugal force, which produces an increase in the moment of inertia. This distortion causes the rotational energy to be less than that of the rigid rotor and it is necessary to add the correction $-hDJ^2(J+1)^2$, where the centrifugal distortion constant D is a small positive constant.
- Details
- Written by: Germán Fernández
- Category: Rotation vibration in diatomic molecules
- Hits: 1187
The energy of a diatomic molecule with the inclusion of the anharmonicity, rotation-vibration interaction and centrifugal distortion terms gives us
\begin{equation} E_{int}=E_{el}+h\nu_e(v+1/2)-h\nu_e x_e(v+1/2)^2+hB_eJ(J+1)-h\alpha_e (v+1/2)J(J+1)-hDJ^2(J+1)^2 \end{equation}
If we add the translational energy to this internal energy, we obtain the total energy of the molecule $E=E_{tr}+E_{int}$



