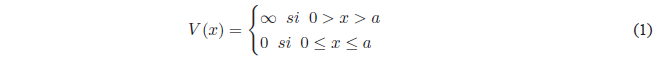The particle in a box | Quantum Mechanics
- Details
- Written by: Germán Fernández
- Category: The particle in a box | Quantum mechanics
- Hits: 50
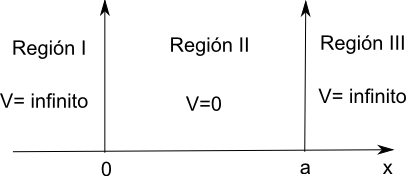
A particle in a box or a particle in a well of infinite potential is called a physical system in which a particle moves under zero potential between two walls of infinite potential. The movement of the particle is confined between both walls, without loss of energy in the collisions. According to classical mechanics, the movement of the particle will be rectilinear and uniform, with changes in the direction of speed (collision) but not in its magnitude.
If the particle is small (quantum) it ceases to comply with Newton's Laws and we must solve the Schrödinger equation to know its behavior. Will the classical results agree with the predictions of quantum mechanics?
- Details
- Written by: Germán Fernández
- Category: The particle in a box | Quantum mechanics
- Hits: 73
Now we are going to introduce a simple quantum mechanical system, where we can apply the concepts introduced in the previous section. This model can be applied to the one-dimensional translational motion of ideal gas molecules, the motion of electrons in metals, and even the motion of pi electrons in unsaturated hydrocarbons.
