Principles and postulates | Quantum Mechanics
- Details
- Written by: Germán Fernández
- Category: Principles and postulates | Quantum mechanics
- Hits: 1169
At the beginning of the 20th century, physicists could not correctly describe the behavior of very small particles such as electrons, atomic nuclei, and molecules. The behavior of these particles is correctly described by a set of physical laws that we call Quantum Mechanics.
At the beginning of the century, a small number of physicists, among whom we can mention Bohr, Einstein, Born, Dirac, Schrödinger, Heisember, De Broglie, Jordan, Pauli, contributed to mathematically formalize the Theory that was practically complete at the end of the decade. 1920's
The study of Quantum Mechanics can be carried out following two different paths. The first way consists of analyzing those physical problems that Classical Mechanics is incapable of solving and that, however, were correctly interpreted by Quantum Mechanics. We can say:
- The Black Body Spectral Radiation Law
- The photoelectric effect.
- The heat capacities of solids.
- The atomic spectrum of the hydrogen atom.
- The Compton Effect
- Details
- Written by: Germán Fernández
- Category: Principles and postulates | Quantum mechanics
- Hits: 1544
Postulate I.- The state of a physical system is described by a function \(\Psi(q,t)\) of the coordinates (q) and time (t). This function, called the state function or wave function, contains all the information that can be determined about the system. In addition, we postulate that \(\Psi(q,t)\) takes simple values, is finite, continuous, with continuous derivatives and integrable square.
Postulate II.- The evolution in time of the state of a system is given by the Schrödinger equation dependent on time:
\begin{equation}i\hbar\frac{\partial\Psi(q,t)}{\partial t}=\hat{H}\Psi(q,t)\end{equation}
Where \(\hbar=\frac{h}{2\pi}\), where h is a universal constant known as Planck's constant, and where \(\hat{H}\) is the Hamiltonian (or Hamiltonian) operator of the system.
For a single particle moving along the x-axis, \(\hat{H}\) is given by:
\begin{equation}\hat{H}=-\frac{\hbar^2}{2m}\frac{\partial}{\partial x}+V(x,t)\end{equation}
- Details
- Written by: Germán Fernández
- Category: Principles and postulates | Quantum mechanics
- Hits: 1187
We will begin by introducing Postulate I of Quantum Mechanics. However, it should be noted that the number of postulates and their order are not unique, but that there are different sets of them that are physically equivalent.
Postulate I.- The state of a physical system is described by a function \(\Psi (q,t)\) of the coordinates \((q)\) and of time \(t\). This function, called the state function or wave function, contains all the information that can be determined about the system. Furthermore, we postulate that \(\Psi (q,t)\) takes simple values, is finite, continuous, with continuous derivatives and integrable square.
The wave function \(\Psi (q,t)\) must be conceived as a mathematical function that gives us information about the system and from which we can calculate its properties.
What information does the wave function provide? Max Born of the Copenhagen School indicated that the squared modulus of the wave function represents the probability density of finding the system in the state with coordinate \(q\). ![]()
- Details
- Written by: Germán Fernández
- Category: Principles and postulates | Quantum mechanics
- Hits: 1133
When the Hamiltonian is independent of time, the state function can be written as a product of a function of time and a function of position. ![]()
Substituting into the time-dependent Schrödinger equation: 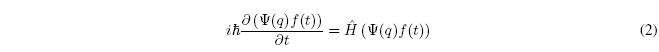
- Details
- Written by: Germán Fernández
- Category: Principles and postulates | Quantum mechanics
- Hits: 1175
An operator acts on a function transforming it into another. Let us take as an example the derivative operator that we represent by \(\hat{D}\), a circumflex is used to indicate that it is an operator, although it can be dispensed with as long as its nature is evident.
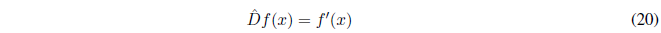
The operator acts on the function f(x) and returns its derivative. Another well-known operator is the integral, the inverse operation of the derivative. But there are also other operators such as:
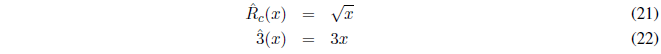
- Details
- Written by: Germán Fernández
- Category: Principles and postulates | Quantum mechanics
- Hits: 1220
Postulate III.- Each physical observable in Quantum Mechanics corresponds to a linear and Hermitian operator. To find such an operator, we write the mechanoclassical expression of the observable in terms of the Cartesian coordinates and the corresponding linear moments. Next, we replace each x-coordinate with the operator $\hat{x}$ (multiply by x) and each momentum \(p_x\) with the operator \(-i\hbar\frac{\partial}{\partial x }\).
Let's see how this postulate works in the construction of the most important operators of Quantum Mechanics.
- Details
- Written by: Germán Fernández
- Category: Principles and postulates | Quantum mechanics
- Hits: 1142
Read more: Measurement of Physical Observables in Quantum Mechanics
- Details
- Written by: Germán Fernández
- Category: Principles and postulates | Quantum mechanics
- Hits: 1109
Eigenvalue equations are those that have the following form:
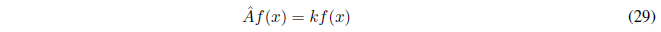
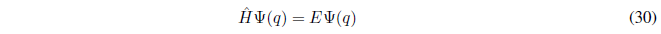
It is simple to show that if a function f(x) is proper to an operator \(\hat{A}\) with eigenvalue k, then all functions of the form cf(x), where c is a constant, are proper to the operator \(\hat{A}\) with eigenvalue k.



