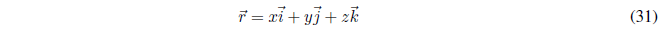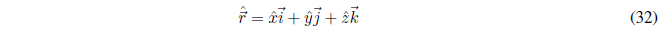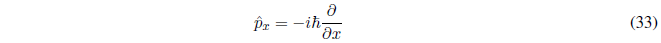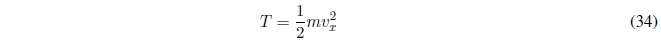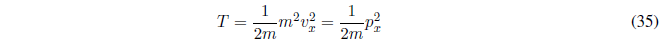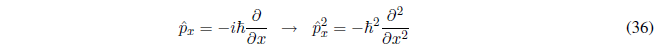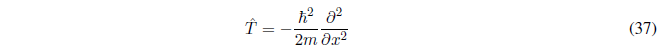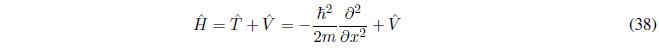Postulate III.- Each physical observable in Quantum Mechanics corresponds to a linear and Hermitian operator. To find such an operator, we write the mechanoclassical expression of the observable in terms of the Cartesian coordinates and the corresponding linear moments. Next, we replace each x-coordinate with the operator $\hat{x}$ (multiply by x) and each momentum \(p_x\) with the operator \(-i\hbar\frac{\partial}{\partial x }\).
Let's see how this postulate works in the construction of the most important operators of Quantum Mechanics.
Position operator of a particle
In Classical Mechanics, the position of a particle moving in one dimension is given by the Cartesian coordinate x. Obtaining the position operator consists of changing the Cartesian coordinate x by the operator \(x\). This operator multiplies the function on which it acts by x.
If we work in three-dimensional space, the position of the particle is given by the position vector:
Obtaining the position operator consists of changing the x,y,z coordinates by the respective operators.
Linear momentum operator of a particle.
In Classical Mechanics the linear momentum is given by the product of the mass by the speed of the particle.
In Quantum Mechanics the linear momentum operator is defined in Postulate III.
Operator kinetic energy of a particle
In Classical Mechanics, kinetic energy is given by the following expression:
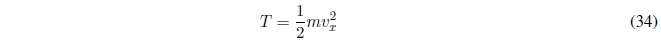
We write this equation in terms of linear momentum \(p_x = mv_x\).
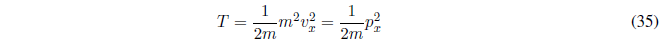
Substituting the amount of movement by:
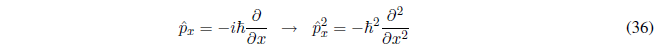
The quantum mechanical operator kinetic energy is obtained
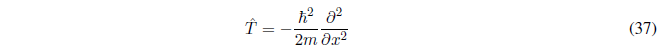
hamiltonian operator
It is the total energy operator of a particle. The Hamiltonian is the sum of the kinetic and potential energies of the particle.