Statistical thermodynamics
- Details
- Written by: Germán Fernández
- Category: statistical thermodynamics
- Hits: 1218
Statistical mechanics is the part of physical chemistry that allows the prediction of thermodynamic properties from the data provided by quantum mechanics. Thus, from microscopic properties of matter (quantum) macroscopic properties such as entropy, heat capacities, internal energy, surface tension, viscosity,... can be obtained.
Statistical thermodynamics assumes that matter is made up of a large number of microscopic components that individually obey quantum mechanics, but collectively obey statistical laws. Statistical thermodynamics establishes a connection between the microscopic description and the macroscopic description of nature.
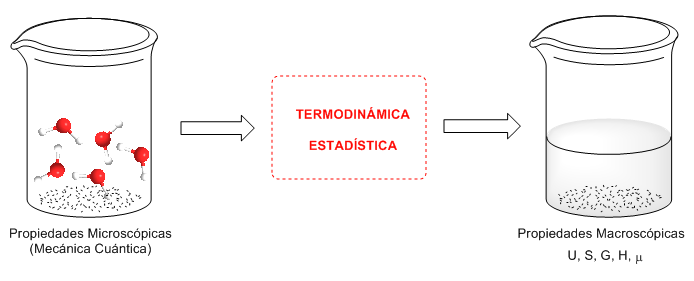
Based on the results at the molecular level that are obtained with quantum mechanics, statistical thermodynamics calculates directly observable properties.
- Details
- Written by: Germán Fernández
- Category: statistical thermodynamics
- Hits: 1447
The particles meet three conditions:
- They are distinguishable from each other (this fact affects entropy)
- They obey the laws of quantum mechanics.
- Furthermore, they do not interact with each other.
MACROSTATE
Statistical mechanics is the link between the microscopic world studied by quantum mechanics, and the macroscopic world studied by classical thermodynamics.
- Details
- Written by: Germán Fernández
- Category: statistical thermodynamics
- Hits: 1238
Let us now calculate the number of microstates associated with any distribution. Let N distinguishable particles be distributed in \(r\) quantum states, as follows: \(N_{1}\) particles in \(\epsilon_{1}\), \(N_{2}\) in \(\epsilon_2 \),........,\(N_r\) in \(\epsilon_r\). The number of microstates of this macrostate is given by the equation:.![]()
- Details
- Written by: Germán Fernández
- Category: statistical thermodynamics
- Hits: 1189
The probability that a system is in a certain distribution will be the greater the greater the number of microstates associated with the distribution. Let \(W_i\) be the number of microstates associated with a certain distribution \(i\), the probability that the system is found in said distribution will be: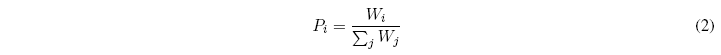
- Details
- Written by: Germán Fernández
- Category: statistical thermodynamics
- Hits: 1562
We are going to calculate from among all the possible macrostates of the system the one that has the largest number of microstates. Thus, the calculation of any thermodynamic quantity is carried out neglecting all the macrostates except the most probable. Mathematically we must calculate $N_{1},N_{2},.....,N_{r}$ so that W takes the maximum value. Where W is given by:
\begin{equation} W=N!\prod_{k}\frac{g_{k}^{N_{k}}}{N_{k}!} \label{ec3} \end{equation}
Taking neperians at (\ref{ec3})
\begin{equation} lnW=lnN!+\sum\left(N_{k}lng_{k}-lnN_{k}!\right) \label{ec4} \end{equation}
Applying in (~\ref{ec4}) the Stirling approximation $lnN!=NlnN-N$:
\begin{equation} lnW=NlnN-N+\sum_{k}N_{k}lng_{k} -\sum_{k}\left(N_{k}lnN_{k}-N_{k}\right) \label{ec5} \end{equation}
Since $\sum_{k}N_{k}=N$ , the equation (\ref{ec5}) can be simplified to
\begin{equation} lnW=NlnN+\sum_{k}N_{k}lng_{k}-\sum_{k}N_{k}lnN_{k} \label{ ec6} \end{equation}
Read more: Most probable distribution: Boltzmann distribution law
- Details
- Written by: Germán Fernández
- Category: statistical thermodynamics
- Hits: 1467
Boltzmann postulated the existence of a relationship between the total entropy of a thermodynamic system and the total number of microstates $(\Omega)$ in which the system can be found.
\begin{equation} S=kln\Omega \label{ec17} \end{equation}
Since $\Omega=\sum_{j}W_{j}\approx{W_{max}}$, where $W_{max} $ represents the most probable macrostate, which for simplicity we will represent by $W$. Thus, the Boltzmann Postulate leaves us with:
\begin{equation} S=klnW \label{ec18} \end{equation}
where $k$ is the Boltzmann constant $k=1.38\cdot10^{-27}J /K$ and $W$ is the macrostate with the largest number of microstates.
- Details
- Written by: Germán Fernández
- Category: statistical thermodynamics
- Hits: 1220
\begin{equation} E=\sum_{i}N_{i}\epsilon_{i}=\sum_{i}\frac{N}{q}g_{i}e^{-\beta{\epsilon_{i }}}\epsilon_{i}=\frac{N}{q}\sum_{i}g_{i}\epsilon_{i}e^{-{\epsilon_{i}}/kT} \label{ec31} \end{equation} Differentiating $q=\sum_{i}g_{i}e^{-\epsilon_{i}/kT}$ with respect to $T$ to volume: \begin{equation} \left(\frac{ \partial{q}}{\partial{T}}\right)_{V}=\frac{1}{kT^2}\sum_{i}g_{i}\epsilon_{i}e^{-\ epsilon_{i}/kT} \label{ec32} \end{equation} Solving the sum of the equation (~\ref{ec32}): \begin{equation} kT^{2}\left(\frac{\partial {q}}{\partial{T}}\right)_{V}=\sum_{i}g_{i}\epsilon_{i}e^{-\epsilon_{i}/kT} \label{ec33} \end{equation} Substituting (~\ref{ec33}) into (~\ref{ec31}) \begin{equation} E=NkT^{2}\left(\frac{\partial{lnq}}{\partial {T}}\right)_{V} \label{ec34} \end{equation}
- Details
- Written by: Germán Fernández
- Category: statistical thermodynamics
- Hits: 1272
We start from the thermodynamic expression for the Helmholtz free energy: \begin{equation} A=E-TS \label{ec35} \end{equation} Substituting $S$ for its value: \begin{equation} A=ET\left (\frac{E}{T}+Nklnq\right)=-NkTlnq \label{ec36} \end{equation} Thus, the Helmholtz equation in statistical mechanics is left: \begin{equation} A=-NkTlnq \label {ec37} \end{equation}
- Details
- Written by: Germán Fernández
- Category: statistical thermodynamics
- Hits: 1270
Since $dA=-SdT-PdV$ to $T=cte$ gives us $P=-\left(\frac{\partial{A}}{\partial{V}}\right)_{T=cte}$
Differentiating the equation $A=-NkTlnq$ with respect to volume and substituting into P gives:
\begin{equation}P=NkT\left(\frac{\partial{lnq}}{\partial{V}}\right)_T=cte}\label{ec38}\end{equation}
- Details
- Written by: Germán Fernández
- Category: statistical thermodynamics
- Hits: 1393
Let us now consider the molecular partition function $q=\sum_{i}g_{i}e^{-\beta{\epsilon_{i}}}$. Molecular energy is the sum of translational, rotational, vibrational, and electronic energy.
\begin{equation} \epsilon_{i}=\epsilon_{tr,n}+\epsilon_{vib,v}+\epsilon_{rot,J}+\epsilon_{ele,u} \label{ec39} \end{equation}
Substituting into the molecular partition function $q$
\begin{equation} q={\sum{g_{i}}{e^{-\beta\left(\epsilon_{tr,n}+\epsilon_{vib ,v}+\epsilon_{rot,J}+\epsilon_{ele,u}\right)}}=\sum_{n}g_{n}e^{-\beta{\epsilon_{tr,n}}} \sum_{v}g_{v}e^{-\beta{\epsilon_{vib,v}}}\sum_{J}g_{J}e^{-\beta{\epsilon_{rot,J}}} \sum_{u}g_{u}e^{-\beta{\epsilon_{ele,u}}}} \label{ec40} \end{equation}
- Details
- Written by: Germán Fernández
- Category: statistical thermodynamics
- Hits: 1468
The translational energy levels are given by the model of the particle in a three-dimensional box.
\begin{equation} \epsilon_{tr}=\frac{h^2}{8m}\left(\frac{n_{x}^{2}}{a^2}+\frac{n_{y}^ {2}}{a^2}+\frac{n_{z}^{2}}{a^2}\right) \end{equation} \begin{equation} q_{tr}=\sum e^{ \beta\epsilon_{tr}}=\sum e^{\frac{\beta h^2}{8m}\left(\frac{n_{x}^{2}}{a^2}+\frac{ n_{y}^{2}}{a^2}+\frac{n_{z}^{2}}{a^2}\right)}=\sum_{n_x =1}^{\infty}e ^{-\frac{\beta h^2n_{x}^{2}}{8ma^2}}\sum_{n_y =1}^{\infty}e^{-\frac{\beta h^2n_{ y}^{2}}{8mb^2}}\sum_{n_z =1}^{\infty}e^{-\frac{\beta h^2n_{z}^{2}}{8mc^2} } \end{equation}
- Details
- Written by: Germán Fernández
- Category: statistical thermodynamics
- Hits: 1330
The pressure of an ideal gas can be obtained from the translational partition function.
\begin{equation} P=NKT\left(\frac{\partial lnq_{tr}}{\partial V}\right)_T \end{equation}
We write the translational partition function:
\begin{equation} q_{tr }=\left(\frac{2\pi mkT}{h^2}\right)^{3/2}V \end{equation}
Taking natural logarithms
\begin{equation} lnq_{tr}=ln\left( \frac{2\pi mkT}{h^2}\right)^{3/2}+lnV \end{equation}
- Details
- Written by: Germán Fernández
- Category: statistical thermodynamics
- Hits: 1916
The energy of the different rotational levels are given by the rigid rotor model: $\epsilon_{rot,J}=\frac{\hbar^2J(J+1)}{2I}$, the degeneracy of the levels is $ g_J=2J+1$
\begin{equation} q_{rot}=\sum_{J=0}^{\infty}g_Je^{\epsilon_{rot,J}/kT}=\sum_{J=0}^ {\infty}(2J+1)e^{-\frac{\hbar^2 J(J+1)}{2IkT}} \end{equation}
We call rotational temperature $\theta_{rot}$ a: $\ theta_{rot}=\frac{\hbar^2}{2Ik}$, has units of temperature (K) but is not temperature in the physical sense. Therefore:
\begin{equation} q_{rot}=\sum_{J=0}^{\infty}(2J+1)e^{-\frac{\theta_{rot}}{{T}}J( J+1)} \end{equation}
If $\frac{\theta_{rot}}{T}$ is small, the separation between rotational levels is small compared to $kT$ and we can approximate the sum by an integral.
\begin{equation} q_{rot}=\int_{0}^{\infty}(2J+1)e^{-\frac{\theta_{rot}}{T}J(J+1)}dJ \end{equation}
- Details
- Written by: Germán Fernández
- Category: statistical thermodynamics
- Hits: 1406
The harmonic oscillator approximation gives $\epsilon_{vib}=\left(v+\frac{1}{2}\right)h\nu$ where $v$ is the vibrational quantum number ranging from $[0,\infty ]$ and there is no degeneracy.
It is usual in statistical mechanics to take the lowest energy level to be zero $\epsilon_{vib}=\left(v+\frac{1}{2}\right)h\nu-\frac{1}{2}h\ nu=vh\nu$
\begin{equation} q_{vib}=\sum_{v}e^{-\beta\epsilon_{vib,v}}=\sum_{v=0}^{\infty}e^{-\beta vh\ nu}=\sum_{0}^{\infty}e^{-\frac{h\nu}{kT}v}=\sum_{0}^{\infty}e^{-\frac{v\theta_ {vib}}{T}} \end{equation} Where $\theta_{vib}=\frac{h\nu}{k}$ called characteristic vibrational temperature.
- Details
- Written by: Germán Fernández
- Category: statistical thermodynamics
- Hits: 1639
We calculate $q_{ele}$ as a sum extended to the electronic energy levels, so we will include the degeneracy $g_{ele}$ of each level. \begin{equation} q_{ele}=\sum_{i}g_{ele,i}e^{-\frac{\epsilon_{ele,i}}{k T}}=g_{ele,0}+g_ {ele,1}e^{-\frac{\epsilon_{ele,1}}{k T}}+g_{ele,2}e^{-\frac{\epsilon_{ele,2}}{k T }}+.... \end{equation} In this last equation we have taken the electronic energy of the fundamental level as zero
- Details
- Written by: Germán Fernández
- Category: statistical thermodynamics
- Hits: 1431
\begin{equation} E=E_{tr}+E_{rot}+E_{vib}+E_{ele} \end{equation}
Calculation of internal translational energy
\begin{equation} E_{tr}=NkT^2 \left(\frac{\partial lnq_{tr}}{\partial T}\right)_{V} \end{equation}
\begin{equation} q_{tr}=\left(\frac{2\pi mkT }{h^2}\right)^{3/2}V \Rightarrow lnq_{tr}=\frac{3}{2}lnT+ln\left(\frac{2\pi mk}{h^2} \right)_V \end{equation}
Differentiating:
\begin{equation} \left(\frac{\partial q_{tr}}{\partial T}\right)_V=\frac{3}{2}\frac{ 1}{T} \end{equation}
\begin{equation} E_{tr}=NkT^2 \cdot \frac{3}{2T}=\frac{3}{2}NkT=\frac{3}{ 2}nRT \end{equation}



