Transport phenomena
- Details
- Written by: Germán Fernández
- Category: transport phenomena
- Hits: 1217
Classical thermodynamics studies the equilibrium properties of systems, the processes being reversible. Now we are going to study systems that are out of equilibrium, in which irreversible processes occur. A system is out of equilibrium because matter or energy is transported between the system and the surroundings, or between different parts of the system. These out-of-equilibrium systems evolve, over time, following irreversible processes towards equilibrium states.
Two examples of irreversible processes are the dissolution of a salt and the transfer of heat between two heat sources at different temperatures. 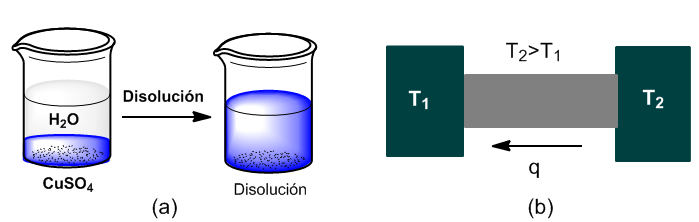
- Details
- Written by: Germán Fernández
- Category: transport phenomena
- Hits: 1244
Fluid flow: There are unbalanced forces in the system, there is no mechanical equilibrium, and parts of the system move.
Newton's Law of viscosity relates the force of friction between the layers of the fluid and the velocity gradient. In this Law a appears a constant of proportionality called viscosity.
\begin{equation} F_x=-\eta A \frac{dv_x}{dz} \end{equation}
- Details
- Written by: Germán Fernández
- Category: transport phenomena
- Hits: 1549
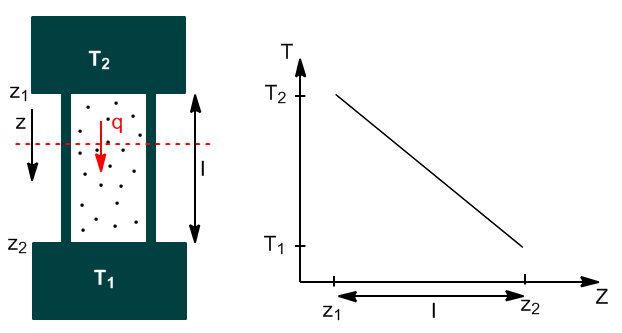
Substance in contact with deposits at different temperatures will eventually reach a steady state in which there will be a uniform temperature gradient dT/dz.
The heat flux dq/dt (measured in J/s) through any plane perpendicular to z is proportional to the cross-sectional area and the temperature gradient.
- Details
- Written by: Germán Fernández
- Category: transport phenomena
- Hits: 1293
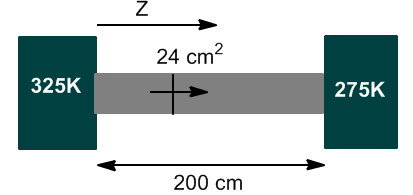
Two heat reservoirs with respective temperatures of 325 and 275 K are brought into contact by an iron rod 200 cm long and 24 cm^2 in cross section. Calculate the heat flux between the reservoirs when the system reaches its steady state. The thermal conductivity of iron at 25ºC is 0.804 J/Kcms.
- Details
- Written by: Germán Fernández
- Category: transport phenomena
- Hits: 1509
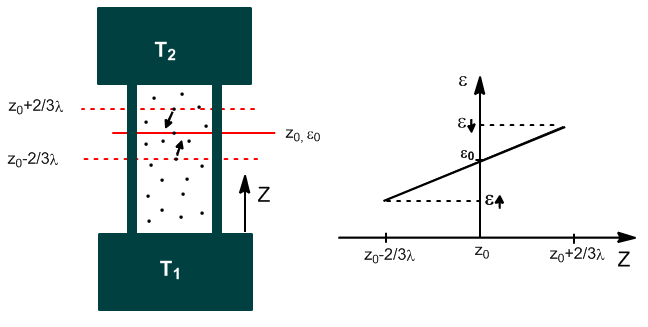
The kinetic theory of gases gives theoretical expressions for thermal conductivity with results consistent with experience. We start from the following approximations:
- Molecules are rigid spheres of diameter d.
- Molecules move at average velocity $\left(\frac{8RT}{\pi M}\right)^{1/2}$
- The average distance traveled by a molecule between two collisions is: $\lambda=\frac{1}{\sqrt{2}\pi d^2}\frac{kT}{P}$
- In each collision the molecular properties adjust to those of that position.
Read more: Evaluation of thermal conductivity through kinetic theory.
- Details
- Written by: Germán Fernández
- Category: transport phenomena
- Hits: 1022
Calculate the thermal conductivity of He at 1 atm and 0ºC and at 10 atm and 100ºC. Use the value of the molecular diameter obtained from viscosity measurements at 1 atm and 0ºC, d=2.2 Anstrong. The experimental value at 0°C and 1 atm is $1.4x10^{-3}$ J/Kcms.
Read more: Example of evaluation of thermal conductivity (k)
- Details
- Written by: Germán Fernández
- Category: transport phenomena
- Hits: 1632
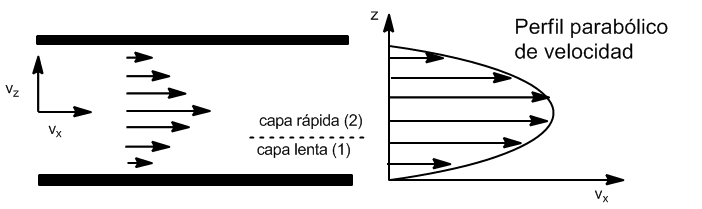
Viscosity is the property that characterizes a fluid's resistance to flow. Fluids that flow easily are low in viscosity. Viscosity is represented by $\eta$, and its units are $Ns/m^2$ Consider a fluid that flows between two large, flat, parallel sheets.
Experience tells us that the speed $v_x$ is maximum in the center and zero on the sheets. The horizontal layers of fluid slide over each other, exerting a frictional force that resists displacement.
The force $F_x$ exerted by the slower moving fluid (1) is proportional to the area of the contact surface, A, and the velocity gradient $\frac{dv_x}{dz}$. The constant of proportionality is the viscosity of the fluid $\eta$
\begin{equation} F_y=-\eta A\frac{dv_y}{dx} \end{equation}
This equation is known as Newton's Law of viscosity. The minus sign indicates that the force of viscosity on the faster moving fluid is opposite to the direction of its motion.
By Newton's Third Law, the faster moving fluid exerts a force $\eta A \frac{dv_y}{dx}$ in the positive $z$ direction on the slower moving fluid.
- Details
- Written by: Germán Fernández
- Category: transport phenomena
- Hits: 1117
We are going to express Newton's Law as a function of linear momentum. We write Newton's Second Law,
\begin{equation} F_x=ma_x=m\frac{dv_x}{dt}=\frac{d(mv_x)}{dt}=\frac{dp_x}{dt} \end{equation}
Substituting into Newton's Law of viscosity:
\begin{equation} \frac{dp_x}{dt}=-\eta A\frac{dv_x}{dz} \end{equation}
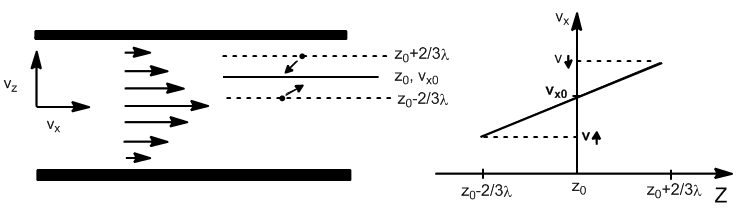
$dp_x/dt$ (flow quantity of movement), represents the variation of the component and of the linear momentum of a layer located on one side inside the fluid, due to its interaction with the fluid on the other side. The molecular explanation of viscosity assumes momentum transport through planes perpendicular to the z axis.
Define the momentum flux per unit area and time: \begin{equation} J_z=\frac{1}{A}\frac{dp_x}{dt}=-\eta\frac{dv_x}{ dz} \end{equation}
- Details
- Written by: Germán Fernández
- Category: transport phenomena
- Hits: 1206
The coefficient of viscosity ($\eta$) depends on temperature, pressure and type of substance. In liquids, the viscosity decreases significantly with increasing temperature due to the weakening of intermolecular forces. In gases, the viscosity tends to increase with increasing temperature.
Since the unit of viscosity $Ns/m^2$ is excessively large, poise and centipoise are defined: $1\;poise=0.1\;Ns/m^2$; $100\;cp=1\;poise$
Viscosities of some fluids: $CH_4$ $\eta=10^{-5}Ns/m^2$; $H_2O$ $\eta=10^{-3}Ns/m^2$; oil $\eta=0.1Ns/m^2$
- Details
- Written by: Germán Fernández
- Category: transport phenomena
- Hits: 1405
It allows to determine the steady laminar flow (dV/dt) for an incompressible fluid, of constant viscosity, through a cylindrical tube of radius r.
Let us consider a fluid flowing through a cylindrical pipe of radius r. Let us take an infinitesimal element of length z and internal radius s, with a pressure $p_1$ at the input and $p_2$ at the output.

We are going to write the forces that act on the fluid layer situated between s and s+ds.
- Hydrostatic pressure forces $(F=PS)$
- Force due to inlet pressure: $F_1=2\pi SdS\cdot P_1$
- Force due to outlet pressure: $F_2=-2\pi SdS\cdot P_2$
- friction forces.
- Friction with the inner part $F_{RI}=-\eta\cdot 2\pi Sdz(dV/dS)_s$. Since the velocity gradient is negative, the friction force is positive since the internal layers go faster and accelerate the fluid layer considered.
- Friction with the outer wall $F_{RE}=\eta\cdot 2\pi (S+dS)dz(dV/dS)_{S+dS}$. This friction force is negative since it opposes the movement of the considered layer.
Once the stationary regime is reached: $\sum\vec{F_i}=0$
\begin{equation} 2\pi SdS\cdot P_1-2\pi SdS\cdot P_2-\eta2\pi Sdz(dv/dS)_S+\eta 2\pi (S+dS)dz(dV/dS)_{ S+dS}=0 \end{equation}
Since $P_2=P_1+dP$
\begin{equation} 2\pi SdS\cdot P_1-2\pi SdS(P_1+dP)-\eta2\pi Sdz(dv /dS)_S+\eta 2\pi (S+dS)dz(dV/dS)_{S+dS}=0 \end{equation}
- Details
- Written by: Germán Fernández
- Category: transport phenomena
- Hits: 1308
We are going to derive an expression for viscosity using the kinetic theory of gases. the deduction is analogous to that made for thermal conductivity, with the exception that momentum is transported instead of heat.
- Details
- Written by: Germán Fernández
- Category: transport phenomena
- Hits: 1112
The viscosities of carbon dioxide at 1 atm and 0, 490, and 850°C are 139, 330, and 436 mP, respectively. Calculate the apparent rigid sphere diameter of carbon dioxide at each of these temperatures.
Read more: Determination of the diameter of the rigid sphere of $CO_2$
- Details
- Written by: Germán Fernández
- Category: transport phenomena
- Hits: 1326
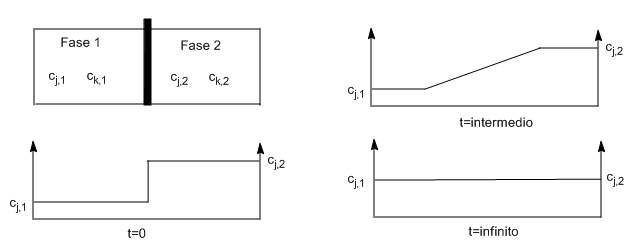
Diffusion: Fick's First Law} If $c_{j,1}\neq c_{j,2}$ and $c_{k,1}\neq c_{k,2}$, removing the partition produces a movement of the species j,k that will reduce or eliminate the difference in concentrations between the two containers.
Diffusion is a macroscopic movement of the components of a system due to concentration differences. If $c_{j,1}$ is less than $c_{j,2}$, there is a net flux of j from 2 to 1 until concentrations and chemical potentials of j and k equalize throughout the cell.
- Details
- Written by: Germán Fernández
- Category: transport phenomena
- Hits: 1444
The deduction is analogous to thermal conductivity or viscosity with the difference that matter is transported.
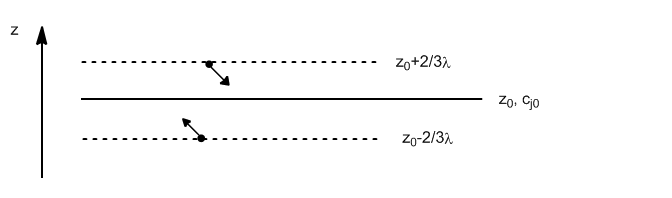
The net flux of matter (in moles) through the $z_0$ plane is given by:
\begin{equation} J_z=J_{\uparrow}-J_{\downarrow}=\frac{dN_{\uparrow}}{N_A }-\frac{dN_{\downarrow}}{N_A} \end{equation}
The number of molecules passing through $z_0$ from below is given by:
\begin{equation} dN_{\uparrow}=\frac{1} {4}\bar{v}\frac{N_{\uparrow}}{V}\frac{N_A}{N_A}=\frac{1}{4}\bar{v}N_A\frac{c_{\uparrow }}{V} \end{equation}



