We are going to derive an expression for viscosity using the kinetic theory of gases. the deduction is analogous to that made for thermal conductivity, with the exception that momentum is transported instead of heat.
\begin{equation} J_z=J_{\uparrow}-J_{\downarrow}=dN_{\uparrow}p_{\uparrow}-dN_{\downarrow}p_{\downarrow} \end{equation}
Given that $dN_{ \uparrow}=dN{\downarrow}=\frac{1}{4}\frac{N}{V}\bar{v}$
\begin{equation} J_z=\frac{1}{4}\frac{ N}{V}\bar{v}(p_{\uparrow}-p_{\downarrow}) \end{equation}
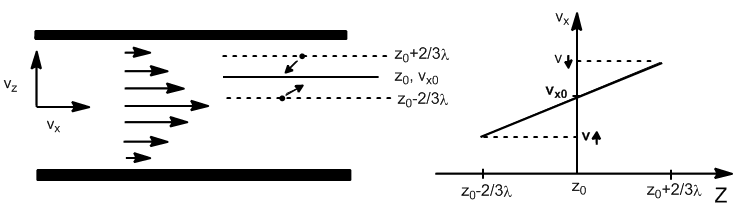
Where, $p_{\uparrow}$ is the momentum of a molecule in the $x_0-2/3\lambda$ plane, and $p_{\downarrow}$ the linear momentum corresponding to the plane $x_0+2/3\lambda$. $J_z$, represents the net flux of linear momentum per unit of area and time.
\begin{equation} p_{\uparrow}=m\left[v_{x0}-\left(\frac{\partial v_x}{\partial z}\right)_0\cdot\frac{2}{3}\lambda\right] \end{equation}
\begin{equation} p_{\downarrow}=m\left[v_{x0}+\left(\frac{\partial v_x}{\partial z}\right)_0\cdot \frac{2}{3}\lambda\right] \end{equation}
Substituting in $J_z$
\begin{equation} J_z=\frac{1}{4}\frac{N}{V}m\left[ v_{x0}-\left(\frac{\partial v_x}{\partial z}\right)_0\cdot\frac{2}{3}\lambda-v_{x0}+\left(\frac{\partial v_x}{\partial z}\right)_0\cdot\frac{2}{3}\lambda\right] \end{equation}
Simplifying
\begin{equation} J_z=\frac{1}{3}\frac{ N}{V}\bar{v}m\lambda\left(\frac{\partial v_x}{\partial z}\right)_0 \end{equation}
Comparing this last equation with $J_z=-\eta\frac {dv_x}{dz}$, we get the value of $\eta$
\begin{equation} \eta =\frac{1}{3}\frac{N}{V}\bar{v}m\lambda \end{equation}
Calling $\rho=N/V$ and $m=M/N_A$, we are left with
\begin{equation} \eta =\frac{1}{3}\bar{v}\lambda\rho\frac {M}{N_A} \end{equation}
A more rigorous treatment leads to the equation :
\begin{equation} \eta=\frac{5\pi}{32}\bar{v}\lambda\rho\frac{M}{N_A} \end{equation}
Equation that is more manageable if we do the following substitutions: $\lambda=\frac{1}{\sqrt{2}\pi d^2}\frac{kT}{P}$; $\rho=\frac{N}{V}=\frac{P}{RT}$ and $\bar{v}=\left(\frac{8kT}{\pi m}\right)^{1/ 2}$:
\begin{equation} \eta =\frac{5}{16\sqrt{\pi}}\frac{{MRT}^{1/2}}{N_Ad^2} \end{equation}



