Ideal solutions
- Details
- Written by: Germán Fernández
- Category: ideal solutions
- Hits: 1161
It is a solution where the molecules of the different species are so similar to each other that the molecules of one component of the solution can replace molecules of another component without changing the spatial structure or the energy of the intermolecular interactions of the solution.
A solution of two components A and B is ideal if the interactions between molecules AA, AB and BB are equal. This situation occurs approximately in isotopic species. $^{12}CH_3Cl$ and $^{13}CH_3Cl$.
This model allows us to approach the study of real solutions. The deviations from the ideal behavior are due to different intermolecular interactions for AA, AB and BB and to differences in size and shape between the A and B molecules.
- Details
- Written by: Germán Fernández
- Category: ideal solutions
- Hits: 1179
Experimentally it is observed that two liquids that are very similar to each other form an ideal solution and present a variation in the Gibbs free energy during the mixing process that is given by:
\begin{equation} \Delta G_{mez}=RT\ sum_{i}n_ilnx_i \label{100}\end{equation}
In the particular case of a binary solution, we are left with:
\begin{equation} \Delta G_{mez}=RT(n_Alnx_A+n_Blnx_B)\label{101} \end{equation}
Chemical potential of an ideal solution
\begin{equation} \Delta G_{mez}=G-G^{\ast}=\sum_{i}n_i\mu_i - \sum_{i}n_i\mu_{i}^{\ast} \end{equation}
Read more: Chemical Potential of a Component in an Ideal Solution
- Details
- Written by: Germán Fernández
- Category: ideal solutions
- Hits: 1180
The normal state of a component in an ideal solution is defined: $\mu_{i}^{0}(T,P)=\mu_{i}^{\ast}(T,P)$ Chemical potential of component i pure at the temperature and pressure of the solution. $(x_i\rightarrow 1)$.
- Details
- Written by: Germán Fernández
- Category: ideal solutions
- Hits: 1097
\begin{equation} \Delta G_{mez}=G-G^{\ast}=\sum_{i}n_i\underbrace{(\mu_i-\mu_{i}^{\ast})}_{RTlnx_i}=RT \sum_{i}lnx_i \end{equation}
$\Delta G_{mez}<0$ for a spontaneous and irreversible process.
\begin{equation} \Delta V_{mez}=\left(\frac{\partial\Delta G_{mez}}{\partial P}\right)_{n_j,P}=0 \end{equation}
At no depend $\Delta G_{mez}$ on the pressure $\Delta V_{mez}$ is null. When mixing two components that form an ideal solution, there is no increase or decrease in volume with respect to the pure components.
\begin{equation} \Delta S_{mez}=-\left(\frac{\partial\Delta G_{mez}}{\partial T}\right)_{n_j,T}=-R\sum_{i} n_ilnx_i \end{equation}
- Details
- Written by: Germán Fernández
- Category: ideal solutions
- Hits: 1276
Consider a system formed by two phases, liquid and gas. The composition of the liquid phase is given by the mole fractions $x_i$ and that of the gas phase by $x_{iv}$. The partial pressures exerted by the components in the gas phase are $P_i$.
Once equilibrium is reached, the chemical potential of each component in the liquid and vapor phases equalize. \begin{equation} \mu_{i,v}=\mu_{i,l} \end{equation} We write the chemical potential of a component $i$ in the vapor phase, assuming that it behaves ideally.
\begin{equation} \mu_{i,v}=\mu_{i,v}^{0}+RTln\frac{P_i}{P^0} \end{equation}
The chemical potential of a component $i$ in the liquid, assuming ideal solution, it will be given by:
\begin{equation} \mu_{i,l}=\mu_{i(l)}^{\ast}+RTlnx_i \end{equation}
Equating both chemical potentials
\begin{equation} \mu_{i,v}^{0}+RTln\frac{P_i}{P^0}=\mu_{i,l}^{\ast}+RTlnx_i \label{130}\end{equation}
- Details
- Written by: Germán Fernández
- Category: ideal solutions
- Hits: 1200
The partial pressure of a component i in the vapor phase is given by the product of its mole fraction in the vapor phase times the total pressure. \begin{equation} P_i=x_{iv}P_{total} \end{equation}
- Details
- Written by: Germán Fernández
- Category: ideal solutions
- Hits: 1223
It is a solution, in which the solute molecules interact only with the solvent ones, due to the high dilution at which the solutes are found.
The chemical potential of the solvent in an ideal dilute solution is given by: \begin{equation} \mu_A=\mu_{A}^{\ast}+RTlnx_A \end{equation} The chemical potential of the solute in an ideal dilute solution , is: \begin{equation} \mu_{i}=\mu_{i}^{0}+RTlnx_i \end{equation}
- Details
- Written by: Germán Fernández
- Category: ideal solutions
- Hits: 1175
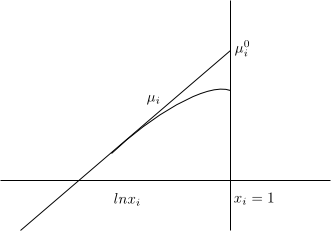
Solvent (A) \begin{equation} \mu_A=\mu_{A}^{0}+RTlnx_A \end{equation} To define the normal state we must cancel the term $RTlnx_A$ and for this we do $x_A \rightarrow 1$ so that $lnx_A \rightarrow 0$ \begin{equation} \mu_{A}^{0}=\mu_{A}^{\ast}(T,P) \end{equation} The normal state of the solvent is defined as a pure solvent at the temperature and pressure of the solution.
Solute (i) \begin{equation} \mu_i=\mu_{i}^{0}+RTlnx_i \end{equation} To define the normal state we must make $x_i \rightarrow 1$, but when $x_i$ increases the solution is no longer ideally dilute. This forces us to define the normal state $\mu_{i}^{0}$ in a fictitious way.
$µ_i^{0}$ is defined as the state in which i is pure and also each molecule of i experiences the same intermolecular forces as in an ideal dilute solution.
- Details
- Written by: Germán Fernández
- Category: ideal solutions
- Hits: 1248
Henry's Law gives us the vapor pressure of a solute in an ideal dilute solution. For the solvent, Raoult's Law still applies. $P_A=x_AP_{A}^{\ast}$
Let be an ideal dilute solution containing a solvent A and solutes (1,2...i). We are going to calculate the pressure exerted by solute i in the gas phase.
Once equilibrium is reached:
\begin{equation} \mu_{i,l}(T,P)=\mu_{i,v}(T,P) \end{equation}
Substituting the chemical potentials for their values
\begin{equation} \mu_{i,l}^{0}(T,P)+RTlnx_{i}=\mu_{i,v}^{0}(T)+RTln\frac{P_i}{P^0 } \end{equation}
Grouping terms and applying properties of natural logarithms
\begin{equation} \frac{\mu_{i,l}^{0}(T,P)-\mu_{i,v}^{0} (T)}{RT}=ln\frac{P_i}{x_iP^0} \end{equation}
Solving for
\begin{equation} \underbrace{P^0e^{\frac{\mu_{i,l}^{ 0}(T,P)-\mu_{i,v}^{0}(T)}{RT}}}_{K_H}=\frac{P_i}{x_i} \end{equation} Where $K_H$ is Henry's constant \begin{equation} P_i=K_Hx_i \end{equation}
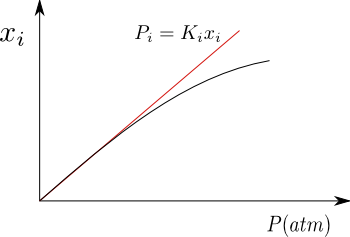
Solubility of gases in liquids
For gases that are poorly soluble in liquids, the solution is close to ideal, fulfilling Henry's Law for the solute. As can be seen in the graph, when the pressure is high, a deviation is produced with respect to Henry, because the solution no longer behaves as an ideal dilute.
- Details
- Written by: Germán Fernández
- Category: ideal solutions
- Hits: 1457
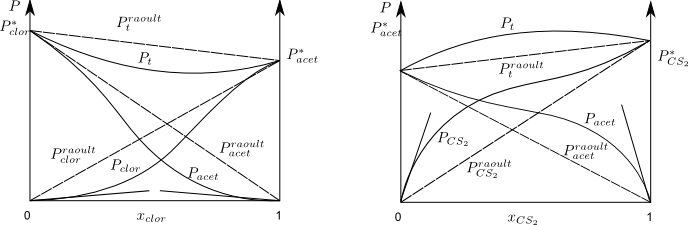
Negative deviations from Raoult's Law.
The acetone-chloroform solution has vapor pressures lower than those predicted by Raoult's Law. This deviation is due to the fact that the intermolecular forces are greater in the solution than in the pure components.
As can be seen from the graph for chloroform mole fractions close to 1, chloroform follows Raoult's Law while acetone follows Henry's Law.
For chloroform mole fractions close to 0, acetone follows Raoult's Law and chloroform follows Henry's.
Positive deviations from Raoult
The acetone-carbon disulfide solution presents vapor pressures higher than those predicted by Raoult, due to the fact that the intermolecular forces in the solution are less than in the pure components.