Henry's Law gives us the vapor pressure of a solute in an ideal dilute solution. For the solvent, Raoult's Law still applies. $P_A=x_AP_{A}^{\ast}$
Let be an ideal dilute solution containing a solvent A and solutes (1,2...i). We are going to calculate the pressure exerted by solute i in the gas phase.
Once equilibrium is reached:
\begin{equation} \mu_{i,l}(T,P)=\mu_{i,v}(T,P) \end{equation}
Substituting the chemical potentials for their values
\begin{equation} \mu_{i,l}^{0}(T,P)+RTlnx_{i}=\mu_{i,v}^{0}(T)+RTln\frac{P_i}{P^0 } \end{equation}
Grouping terms and applying properties of natural logarithms
\begin{equation} \frac{\mu_{i,l}^{0}(T,P)-\mu_{i,v}^{0} (T)}{RT}=ln\frac{P_i}{x_iP^0} \end{equation}
Solving for
\begin{equation} \underbrace{P^0e^{\frac{\mu_{i,l}^{ 0}(T,P)-\mu_{i,v}^{0}(T)}{RT}}}_{K_H}=\frac{P_i}{x_i} \end{equation} Where $K_H$ is Henry's constant \begin{equation} P_i=K_Hx_i \end{equation}
Solubility of gases in liquids
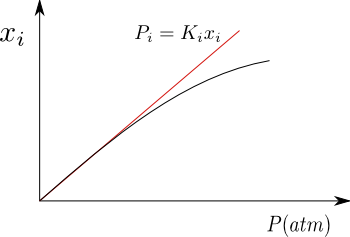
For gases that are poorly soluble in liquids, the solution is close to ideal, fulfilling Henry's Law for the solute. As can be seen in the graph, when the pressure is high, a deviation is produced with respect to Henry, because the solution no longer behaves as an ideal dilute.