Material equilibrium
- Details
- Written by: Germán Fernández
- Category: material balance
- Hits: 1164
Material equilibrium is reached when a system is in chemical equilibrium and in phase equilibrium. Chemical equilibrium implies that all reactions occurring in the system have reached equilibrium. Phase equilibrium implies the absence of a net flow of matter from some phases of the system to others.
The second law of thermodynamics provides us with an equilibrium criterion for isolated systems. In addition, it allows us to determine if a process is possible. The processes that involve an increase in the entropy of the universe $S_{uni}$ are spontaneous and irreversible. Those processes with $\Delta S_{uni}=0$ are reversible and very difficult to perform. Processes involving a decrease in entropy $\Delta S_{uni}<0$ do not take place.
In this section we will see two functions that allow us to predict the spontaneity of a process in a more general way than entropy. These new state functions are: the Helmholtz function $A=U-TS$ and the Gibbs function $G=H-TS$
- Details
- Written by: Germán Fernández
- Category: material balance
- Hits: 1390
The equilibrium criterion in an isolated system is that its entropy is maximum. An isolated system that is not in material equilibrium exhibits chemical reactions or flow of matter between phases. These irreversible processes produce an increase in the entropy of the system. When these processes cease, entropy reaches its highest value and the system is in equilibrium.
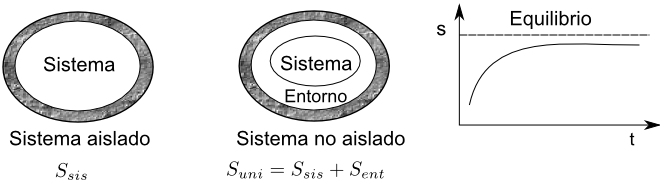
For closed systems, the equilibrium condition is the maximization of the entropy of the system plus that of its surroundings ($S_{sis}+S_{ent})$ maximum in equilibrium.
Using entropy as a criterion of spontenity forces us to know how the entropy of the environment varies in the case of closed systems. Since it is easier to work with the thermodynamic properties of the system, forgetting about the environment, we must look for another thermodynamic function that gives us an equilibrium criterion.
- Details
- Written by: Germán Fernández
- Category: material balance
- Hits: 1364
In this section we will obtain the expressions for the differentials dH, dA, dG using the relation $dU=TdS-PdV$ from the definitions $H=U+PV$, $A=U-TS$ and $G=H- TS$.
We start by getting dH: \begin{equation} dH=d(U+PV)=dU+PdV+VdP=TdS-PdV+PdV+VdP=TdS+VdP \end{equation} Similarly we get dA and dG. \begin{equation} dA=d(U-TS)=dU-SdT-TdS=\cancel{TdS}-PdV-SdT-\cancel{TdS}=-SdT-PdV \end{equation} \begin{equation} dG=d(H-TS)=dH-TdS-SdT=\cancel{TdS}+VdP-\cancel{TdS}-SdT=-SdT+VdP \end{equation} Therefore the Gibbs equations are: \begin{eqnarray} dU & = & TdS - PdV\\ dH & = & TdS+VdP\\ dA & = & -SdT-PdV\\ dG & = & -SdT+VdP \end{eqnarray}
- Details
- Written by: Germán Fernández
- Category: material balance
- Hits: 1260
To obtain the Maxwell relations we will use the Euler reciprocity relation. If $dz=Mdx+Ndy$ the following relationship holds: \begin{equation} \left(\frac{\partial M}{\partial y}\right)_x=\left(\frac{\partial N}{ \partial x}\right)_y \end{equation} Writing the Gibbs equation for dU: \begin{equation} dU=TdS-PdV=Mdx+Ndy \end{equation} Applying the Euler reciprocity relation we obtain one of Maxwell's equations.
- Details
- Written by: Germán Fernández
- Category: material balance
- Hits: 1156
Using the equation (\ref{7}) we will obtain the equilibrium criterion at constant T and V. We must bear in mind that these conditions assume $dV=0$ and $dT=0$. Substituting in (\ref{7}) $dw=-PdV$ in addition to adding and subtracting $SdT$ is obtained. \begin{equation} dU\leq TdS +SdT-sdT -PdV \end{equation} Since $d(TS)=TdS+SdT$ the previous equation remains: \begin{equation} dU\leq d(TS)- SdT-PdV \end{equation} Passing the term $d(TS)$ to the first term of the inequality \begin{equation} d(U-TS)\leq -SdT-PdV \end{equation} Holding T and V constant during the process, $dT=dV=0$ \begin{equation} d(U-TS)\leq 0 \end{equation} This means that during an irreversible process (chemical reaction or mass transfer between phases) the function of state $U-TS$ decreases until equilibrium. Once equilibrium is reached, this function remains constant. Therefore, the equilibrium criterion at constant T, V consists in minimizing the state function $U-TS$. This function is called the Helmholtz free energy, and is represented by A. \begin{equation} A=U-TS \end{equation}
- Details
- Written by: Germán Fernández
- Category: material balance
- Hits: 1163
All relationships between state functions can be obtained from six basic equations. \begin{eqnarray} dU & = & TdS - PdV\\ H & = & U +PV\\ A & = & U-TS\\ G & = & H-TS\\ C_V & = & \frac{dq_v} {dT}=\left(\frac{\partial U}{\partial T}\right)_v\\ C_P & = & \frac{dq_p}{dT}=\left(\frac{\partial H}{\partial T}\right)_P \end{eqnarray}
- Details
- Written by: Germán Fernández
- Category: material balance
- Hits: 1189
Dependence of U with respect to V
Let's calculate $\left(\frac{\partial U}{\partial V}\right)_T$ using the Gibbs equation $dU=TdS-PdV$.
We divide the Gibbs equation by dV keeping the temperature constant :
\begin{equation} \left(\frac{\partial U}{\partial V}\right)_T=T\left(\frac{\partial S}{\partial V}\right)_T-P \end{equation}
Using Maxwell's relation, $\left(\frac{\partial S}{\partial V}\right)_T=\left(\frac{\partial P}{\partial T}\right)_V$ , we get:
\begin{equation} \left(\frac{\partial U}{\partial V}\right)_T=T\left(\frac{\partial P}{\partial T}\right)_V- P=\frac{\alpha T}{\kappa}-P \end{equation}
In the above equation we used the relation: $\left(\frac{\partial P}{\partial T}\right)_V=\frac{\alpha}{\kappa}$
Read more: Dependence of Internal Energy with Volume and Temperature
- Details
- Written by: Germán Fernández
- Category: material balance
- Hits: 1128
Dependence of H on T
Keeping the pressure constant, the dependence of H on temperature is given by the expression: \begin{equation} \left(\frac{\partial H}{\partial T}\right)_P=C_P \end{equation}
Dependence of H with P
To calculate $\left(\frac{\partial H}{\partial P}\right)_T$ we use the Gibbs equation $dH=TdS+VdP$ keeping the temperature constant. \begin{equation} \left(\frac{\partial H}{\partial P}\right)_T=T\left(\frac{\partial S}{\partial P}\right)_T + V=-TV \alpha +V \end{equation} In the last step, Maxwell's equations were used.
- Details
- Written by: Germán Fernández
- Category: material balance
- Hits: 1163
Dependence of S on T
Dividing the ratio $dS=dq/T$ by dT and keeping the pressure constant gives the desired ratio.
\begin{equation} \left(\frac{\partial S}{\partial P}\right)_T=\frac{C_P}{T} \end{equation}
Dependence of S with respect to P
Using the Gibbs equation $dG=-SdT-VdP$ and one of Maxwell's relations, we obtain:
\begin{equation} \left(\frac{\partial S}{\partial P}\right)_T=-\left(\frac{\partial V}{\partial T}\right)_P=-\alpha V \end{equation}
- Details
- Written by: Germán Fernández
- Category: material balance
- Hits: 1143
Setting dP=0 in the Gibbs equation $dG=-SdT+VdP$ gives:
\begin{equation} \left(\frac{\partial G}{\partial T}\right)_P=-S \end{equation}
Putting dT=0 in the Gibbs equation gives:
\begin{equation} \left(\frac{\partial G}{\partial P}\right)_T=V \end{equation}
- Details
- Written by: Germán Fernández
- Category: material balance
- Hits: 1120
The difference between $C_p$ and $C_v$ is given by: \begin{equation} C_p-C_v=\left[\left(\frac{\partial U}{\partial V}\right)_T+P\right] \left(\frac{\partial V}{\partial T}\right)_P \end{equation} Substituting into the above equation, $\left(\frac{\partial U}{\partial V}\right)_T =\frac{\alpha}{\kappa}TP$, gives us: \begin{equation} C_p-C_v=\left[\frac{\alpha}{\kappa}T-P+P\right]V\frac {1}{V}\left(\frac{\partial V}{\partial T}\right)_P \end{equation} Simplifying: \begin{equation} C_p-C_v=\frac{TV\alpha^2} {\kappa} \end{equation}
- Details
- Written by: Germán Fernández
- Category: material balance
- Hits: 1127
Let us consider a closed system of constant composition that goes from a state $(P_1, T_1)$ to $(P_2, T_2)$, regardless of the trajectory followed or irreversibility. Consider the entropy of this system as a function of T,P, $S=S(T,P)$. Differentiating: \begin{equation} dS=\left(\frac{\partial S}{\partial T}\right)_PdT+\left(\frac{\partial S}{\partial P}\right)_TdP=\frac {C_P}{T}dT-\alpha VdP \end{equation} Integrating from an initial state (1) to the final state (2) we obtain the entropy change. \begin{equation} \Delta S=\int_{T_1}^{T_2}\frac{C_p}{T}dT-\int_{P_1}^{P_2}\alpha VdP \end{equation} Since entropy is a As a state function, the entropy change between two states does not depend on the path followed. The first integral is calculated at the pressure $P_1$ while the second is evaluated at the temperature $T_2$
- Details
- Written by: Germán Fernández
- Category: material balance
- Hits: 1249
Starting from the relation $dH=(\partial H/\partial T)_P dT+(\partial H/\partial P)_T dP$, we obtain: \begin{equation} \Delta H=\int_{1}^{ 2}C_pdT + \int_{1}^{2}(V-TV\alpha)dP \end{equation} $\Delta U$ can be obtained by the expression: $\Delta U=\Delta H -\Delta(PV )$
- Details
- Written by: Germán Fernández
- Category: material balance
- Hits: 1172
To calculate $\Delta G$, first obtain $\Delta H$ and $\Delta S$ and then use: $\Delta G = \Delta H - T\Delta S$, valid for an isothermal process.
Another alternative is to integrate the equation, $(\partial G/\partial P)_T=V$. \begin{equation} \Delta G=\int_{P_1}^{P_2}VdP \end{equation} In the particular case that P and T are constants $\Delta H = q$ and $\Delta S = q/ T$, therefore $\Delta G =0$. An example of this situation is the reversible phase change.
The calculation of $\Delta A$ is done with the expression $\Delta A = \Delta U - T\Delta S$, or with $\Delta A=-\int_{1}^{2}PdV$
- Details
- Written by: Germán Fernández
- Category: material balance
- Hits: 1136
If a system is open, the number of moles of the components changes, $n_i$. The functions $U, H, A, G$ become dependent on $(T,P,n_i)$, $G=G(T,P,n_1,n_2,n_3,.....,n_k)$
\begin{equation} dG=\left(\frac{\partial G}{\partial T}\right)_{p,n_j}dT + \left(\frac{\partial G}{\partial P}\right) {T,n_j}dP + \left(\frac{\partial G}{\partial n_1}\right)_{T,p,n_{j\neq n_1}}dn_1 + .......+ \left(\frac{\partial G}{\partial n_k}\right)_{p,n_{j \neq k}}dT \end{equation}
Whereas, $\left(\frac{\partial G} {\partial T}\right)_{P,n_i}=-S$ and $\left(\frac{\partial G}{\partial P}\right)_{T,n_i}=V$, the equation above can be written as: \begin{equation} dG=-SdT+VdP+\sum_{i=1}^{k}\left(\frac{\partial G}{\partial n_i}\right)_{T, P,n_{j \neq n_i}}dn_i \end{equation}
- Details
- Written by: Germán Fernández
- Category: material balance
- Hits: 1081
Let $G$ be the total Gibbs energy of a system. Let $G^{\alpha}$ be the Gibbs free energy of phase $\alpha$. The Gibbs free energy change for phase $\alpha$ will be given by: \begin{equation} dG^{\alpha}=-S^{\alpha}dT+V^{\alpha}dP+\sum_{ i}\mu_{i}^{\alpha}dn_{i}^{\alpha} \end{equation} The total Gibbs free energy change will be given by: \begin{equation} dG=-\sum_{ \alpha}S^{\alpha}dT+\sum_{\alpha}V^{\alpha}dP+\sum_{\alpha}\sum_{i}\mu_{i}^{\alpha}dn_{i}^{ \alpha} \end{equation} \begin{equation} dG=-SdT+VdP+\sum_{\alpha}\sum_{i}\mu_{i}^{\alpha}dn_{i}^{\alpha} \end{equation}
- Details
- Written by: Germán Fernández
- Category: material balance
- Hits: 1032
The material equilibrium condition at constant T, P is obtained by setting, $dG=0$ \begin{equation} \sum_{\alpha}\sum_{i}\mu_{i}^{\alpha}dn_{i}^ {\alpha} \end{equation} At constant temperature and volume the equilibrium condition is given by $dA=0$ \begin{equation} dA = -SdT -PdV +\sum_{\alpha}\sum_{i}\mu_{i}^{\alpha}dn_{i}^{\alpha} \end{equation} making $dA=dT=dV=0$ obtains the same equilibrium condition as in the case of working at T,P constants.
- Details
- Written by: Germán Fernández
- Category: material balance
- Hits: 1154
The chemical potential $\mu_{i}$ of component i in a one-phase system is given by: \begin{equation} \mu_i =\left(\frac{\partial G}{\partial n_i}\right)_ {T,P,n_{j\neq i}} \end{equation} The chemical potential of a substance i in phase $\alpha$ is a state function that depends on temperature, pressure, and phase composition, $ µ_{i}^{\alpha} = µ_{i}^{\alpha}(T^{\alpha}, P^{\alpha}, x_{1}^{\alpha}, x_{2} ^{\alpha}...)$
For a pure substance the chemical potential coincides with the molar Gibbs free energy $\mu_{i}=\left(\frac{\partial G}{\partial n_i}\right)_{T,P}=\bar{ G}_i$
- Details
- Written by: Germán Fernández
- Category: material balance
- Hits: 1156
In a closed system in thermal and mechanical equilibrium with PV work only, the phase equilibrium condition is that the chemical potential of a given component is the same for all phases of the system. \begin{equation} \mu_{j}^{\beta}=\mu_{j}^{\delta} \end{equation}
- Details
- Written by: Germán Fernández
- Category: material balance
- Hits: 1183
The equilibrium condition of a chemical reaction, $\nu_{1}A_{1}+\nu_{2}A_{2}+.....\rightarrow 0$, in a closed system is: \begin{equation} \sum_{i}\nu_{i}\mu_{i}=0 \end{equation} During the course of a chemical reaction, the change in the number of moles of each substance is proportional to the stoichiometric coefficient $\nu$ , being the constant of proportionality the same for all species. This constant is called the degree of progress of the reaction $\xi$ and is defined as: \begin{equation} \xi =\frac{n_i -n_{i,0}}{\nu_i} \end{equation}



