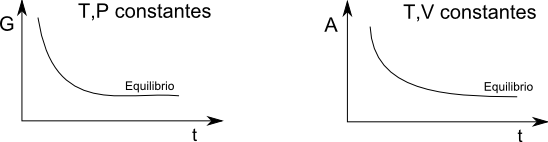
Using the equation (\ref{7}) we will obtain the equilibrium criterion at constant T and V. We must bear in mind that these conditions assume $dV=0$ and $dT=0$. Substituting in (\ref{7}) $dw=-PdV$ in addition to adding and subtracting $SdT$ is obtained. \begin{equation} dU\leq TdS +SdT-sdT -PdV \end{equation} Since $d(TS)=TdS+SdT$ the previous equation remains: \begin{equation} dU\leq d(TS)- SdT-PdV \end{equation} Passing the term $d(TS)$ to the first term of the inequality \begin{equation} d(U-TS)\leq -SdT-PdV \end{equation} Holding T and V constant during the process, $dT=dV=0$ \begin{equation} d(U-TS)\leq 0 \end{equation} This means that during an irreversible process (chemical reaction or mass transfer between phases) the function of state $U-TS$ decreases until equilibrium. Once equilibrium is reached, this function remains constant. Therefore, the equilibrium criterion at constant T, V consists in minimizing the state function $U-TS$. This function is called the Helmholtz free energy, and is represented by A. \begin{equation} A=U-TS \end{equation}
Finally we have to find the material equilibrium criterion at constant T, P. Adding and subtracting from the equation (\ref{7}) $SdT$ and VdP: \begin{equation} dU \leq TdS+SdT-SdT-PdV+VdP-VdP \end{equation} Grouping: \begin{equation} dU\leq d(TS)-SdT-d(PV)+VdP \end{equation} \begin{equation} d(U+PV-TS)\leq-SdT-VdP \end{equation} Given that $ dT=dV=0$ and that $H=U+PV$ \begin{equation} d(H-TS)\leq 0 \end{equation} The state function $H-TS$ is called the Gibbs free energy and is represented by G. \begin{equation} G=H-TS \end{equation} The function G decreases as the thermodynamic system approaches material equilibrium, reaching its minimum value at equilibrium.