Introduction to spectroscopy
- Details
- Written by: Germán Fernández
- Category: Introduction to spectroscopy
- Hits: 1943
Spectroscopy provides most of the information about the energy levels in atoms and molecules. This information is obtained by studying the absorption and emission of electromagnetic radiation by matter.
In this chapter we will study the rotational and vibrational spectra of diatomic and polyatomic molecules, electronic spectra, and nuclear magnetic resonance spectra.
Spectroscopy has application in all fields of chemistry:
- It allows the determination of angles, bond lengths, conformations and vibration frequencies in molecules.
- Organic chemistry uses magnetic resonance spectroscopy to determine the structure of organic compounds.
- In kinetics, spectroscopic methods are used in order to know the variation of a reactant or product over time.
- Analytical chemistry used spectroscopy to determine the composition of a sample.
- It is even possible to know the composition of distant planets and stars by studying the light that reaches us.
- Details
- Written by: Germán Fernández
- Category: Introduction to spectroscopy
- Hits: 1246
Electromagnetic waves are formed by electric and magnetic fields that oscillate perpendicular to each other and perpedicular to the direction of propagation of the wave. Electromagnetic radiation propagates at the speed of \(2,998\times 10^8\;m/s\), coinciding with the speed of light. 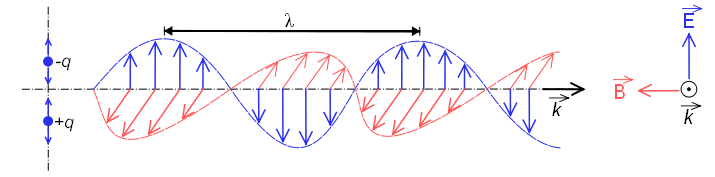
In this figure you can see an electromagnetic wave polarized in the plane (the vectors of the electric field are contained in the same plane). This type of wave is produced by the oscillation of an electric charge moving in a straight line. The radiation emitted by atoms or molecules when heated does not present polarization, due to the random movement that they present.
- Details
- Written by: Germán Fernández
- Category: Introduction to spectroscopy
- Hits: 1252
The electromagnetic spectrum is called the energy distribution of the set of electromagnetic waves.
The electromagnetic spectrum extends from radiation of shorter wavelengths, such as gamma rays and X-rays, through ultraviolet light, visible light and infrared rays, to electromagnetic waves of longer wavelengths, such as radio waves. The limit for the smallest possible wavelength is believed to be the Planck length while the maximum limit would be the size of the Universe. 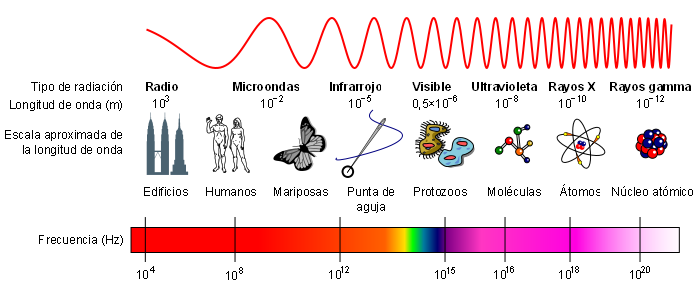
- Details
- Written by: Germán Fernández
- Category: Introduction to spectroscopy
- Hits: 1215
Regardless of its frequency, any electromagnetic radiation (light) travels at \(c=3\times 10^8\; m/s\) in a vacuum. However, the speed of light decreases to a value \(c_B\) when propagating through a homogeneous material medium. The spare part index \(n_B\) is defined as the quotient between both speeds: ![]()
The following table shows refractive index values for different substances. The sodium D line (589.3 nm) at 25°C and 1 atm is used as radiation. 
- Details
- Written by: Germán Fernández
- Category: Introduction to spectroscopy
- Hits: 1147
When a light beam passes through a glass prism, the different monochromatic radiations are all the more deflected by refraction the shorter their wavelength. In this way, the red rays are less deflected than the purple ones and the primitive beam of white light becomes an electromagnetic spectrum. An example is the scattering of white light from the sun into the colors red, orange, yellow, green, blue and violet.

Radiation-Matter Interaction according to Quantum Mechanics
In 1905 Einstein proposed that light was made up of particles, called photons, with energy $h\nu$. Photons are absorbed or emitted by matter producing transitions between different allowed energy levels.
- Details
- Written by: Germán Fernández
- Category: Introduction to spectroscopy
- Hits: 1138
Spectroscopy studies the emission or absorption of electromagnetic radiation by matter. Spectroscopy also studies the scattering of light and the rotation of the plane of polarization produced by optically active substances.
Specter Types
The series of frequencies absorbed by a sample is called an absorption spectrum. The series of frequencies emitted by a sample is called the emission spectrum. Spectra can also be classified into:
- Line spectra are made up of discrete frequencies that appear in the form of bands. These spectra are obtained by heating a gas that is not at very high pressure.

- Continuous spectra are formed by a continuous range of frequencies. Solids and liquids when heated usually give rise to continuous spectra.

- Details
- Written by: Germán Fernández
- Category: Introduction to spectroscopy
- Hits: 1290
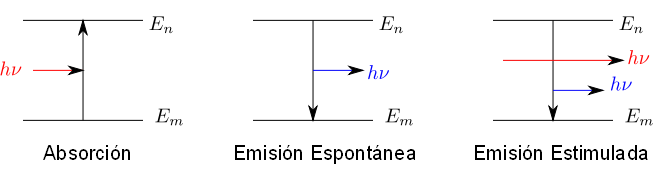
Absorption spectra are produced when matter absorbs a photon of frequency $\nu$ whose energy is $h\nu$ and passes from a lower energy state $E_m$ to a higher energy state $E_n$. It must be true that the energy difference between these states is equal to the energy of the absorbed photon, $E_n - E_m = h\nu$.
In spontaneous emission spectra a molecule passes from an energy state $E_n$ to a lower energy state $E_m$, emitting a photon of energy $E_n - E_m =h\nu$
The emission of radiation by matter can be enhanced by exposure to electromagnetic radiation. In this case we speak of stimulated emission. Exposing the molecule to electromagnetic radiation of frequency $E_n - E_m =h\nu$ increases the probability that the transition from state n to state m occurs.
- Details
- Written by: Germán Fernández
- Category: Introduction to spectroscopy
- Hits: 1555
It can be shown that the probability of absorption or emission between two stationary states m and n is proportional to the square of the integral $\mu_{mn}$ called the dipole transition moment.
\begin{equation} \mu_{mn}=\int{\psi^{\ast}_m\hat{\mu}\psi_n}dq \end{equation}
Being $\hat{\mu}$ the electric dipole moment, defined as: $\hat{\mu}=\sum_{i}Q_ir_i$
- When $\mu_{mn}=0$, the transition between states m and n has zero probability, transition forbidden.
- When $\mu_{mn}\neq 0$, the transition between states m and n is allowed.
Example: For the particle in a box, obtain the dipole transition moment and obtain the selection rule



