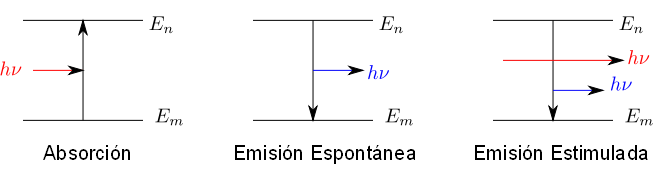
Absorption spectra are produced when matter absorbs a photon of frequency $\nu$ whose energy is $h\nu$ and passes from a lower energy state $E_m$ to a higher energy state $E_n$. It must be true that the energy difference between these states is equal to the energy of the absorbed photon, $E_n - E_m = h\nu$.
In spontaneous emission spectra a molecule passes from an energy state $E_n$ to a lower energy state $E_m$, emitting a photon of energy $E_n - E_m =h\nu$
The emission of radiation by matter can be enhanced by exposure to electromagnetic radiation. In this case we speak of stimulated emission. Exposing the molecule to electromagnetic radiation of frequency $E_n - E_m =h\nu$ increases the probability that the transition from state n to state m occurs.
From what has been said above, it can be deduced that electromagnetic radiation must have an adequate frequency to produce a transition between states. The electronic states of a molecule are more widely spaced than the vibrational ones, and these in turn are more widely spaced than the rotational ones. Electronic transitions are produced by absorption in the ultraviolet-visible (UV) region (energy radiation). Vibrational transitions produce absorption in the infrared (IR) region. Finally, rotational transitions are produced by absorption in the microwave region.
True or false?
(a) When a molecule absorbs photons there is a transition to a steady state of energy $E_k$, the absorption frequency $\nu$ satisfies $E_k=h\nu$.
(b) When a molecule emits a photon of frequency $\nu$, it undergoes an energy change that is given by $\Delta E=h\nu$.
(c) When a molecule absorbs a photon of frequency $\nu$, it experiences an energy change given by $\Delta E=h\nu$.
(d) The longer wavelength of a transition corresponds to the smaller difference in energy between the two levels involved in the transition.
(e) Exposing a molecule in state n to electromagnetic radiation of frequency $\nu=(E_n -E_m)/h\nu$ will increase the probability that the molecule will transition to the state of lower energy m with emission of a photon of frequency $\nu$.}



