Harmonic oscillator | Quantum mechanics
- Details
- Written by: Germán Fernández
- Category: Harmonic oscillator | Quantum mechanics
- Hits: 150
We set up the Schödinger equation:
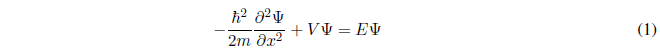
The harmonic oscillator is subjected to a potential of the type: \(V(x)=\frac{1}{2}kx^2\)
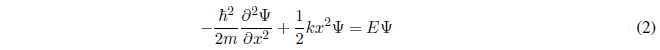
Solving for the derivative of higher degree, equation (2) can be written:
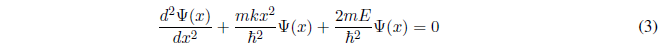
- Details
- Written by: Germán Fernández
- Category: Harmonic oscillator | Quantum mechanics
- Hits: 176
The harmonic oscillator is a physical system in which a mass oscillates around an equilibrium position subjected to an elastic potential \(V(x)=\frac{1}{2}kx^2\). The oscillation of the atoms in a molecule can be studied using the quantum version of this model. Solving the Schrödinger equation gives us the energy levels and the wave function.
- Details
- Written by: Germán Fernández
- Category: Harmonic oscillator | Quantum mechanics
- Hits: 156
The differential equation (16) has a solution of the type:
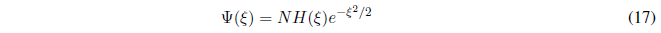
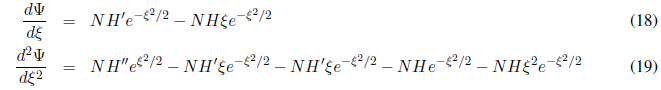
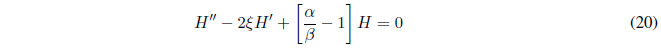
- Details
- Written by: Germán Fernández
- Category: Harmonic oscillator | Quantum mechanics
- Hits: 144
Some expressions that allow us to calculate the Hermite polynomials are: \begin{equation}\label{ec-34} H_v(\xi)=(2\xi)^vv(v-1)(2\xi)^{v- 2}+\frac{v(v-1)(v-2)(v-3)}{2}(2\xi)^{v-4}+...... \end{equation} The Equation (\ref{ec-34}) can be written more compactly as: \begin{equation}\label{ec-35} H_v(\xi)=\sum_{k=0}^{v}(- 1)^k\frac{v!}{k!(v-2k)!}(2\xi)^{v-2k} \end{equation}
- Details
- Written by: Germán Fernández
- Category: Harmonic oscillator | Quantum mechanics
- Hits: 157
The wave functions of the harmonic oscillator are given by the equation (\ref{ec17}), where N is the normalization constant, which we can calculate with the following equation: \begin{equation}\label{ec-43} \int_ {-\infty}^{+\infty}\Psi_{v}^{\ast}(x)\Psi_{v}(x)dx=1 \end{equation} The normalization of the wave function for a state general $v$ gives us the following result: \begin{equation} N_v =\left(2^vv!\right)^{-1/2}\left(\frac{\beta}{\pi}\right) ^{1/4} \end{equation}
- Details
- Written by: Germán Fernández
- Category: Harmonic oscillator | Quantum mechanics
- Hits: 136
- For the ground state of the one-dimensional harmonic oscillator, find the average value of the kinetic and potential energies. Check that <T>=<V> in this case. Find the most probable position of the particle for said wave function and verify that the uncertainty principle is satisfied. Data:$\int_{0}^{\infty}x^2 e^{-\alpha x^2}dx=\pi^{1/2}/4\alpha^{3/2}$
- Using the Rodrigues formula, generate the polynomials with $v=0,1,2,3....$
- The three-dimensional harmonic oscillator has the potential energy function $V(x,yz)=k_x \frac{x^2}{2} + k_y \frac{y^2}{2} + k_z \frac{z^2} {2}$, where $k_x$, $k_y$, and $k_z$ are three force constants. Using the method of separation of variables, find the eigenfunctions and the eigenvalues of the energy of said oscillator.