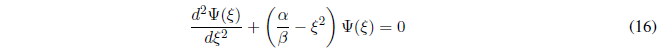We set up the Schödinger equation:
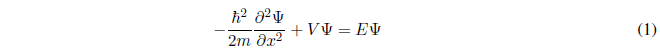
The harmonic oscillator is subjected to a potential of the type: \(V(x)=\frac{1}{2}kx^2\)
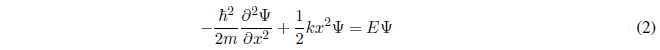
Solving for the derivative of higher degree, equation (2) can be written:
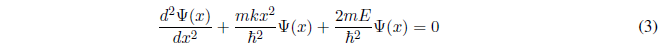
We simplify equation (3) by defining the following magnitudes:
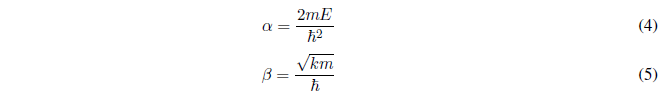
Substituting (4) and (5) into (3):
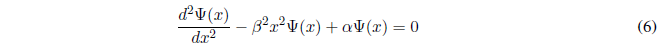
Solving equation (6) requires the following change of variable:
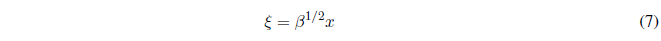
Applying the chain rule:
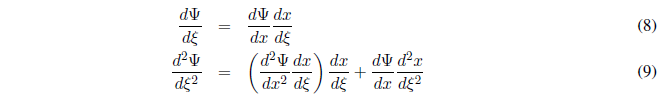
Solving for x from (7) and differentiating with respect to \(\xi\) we obtain:
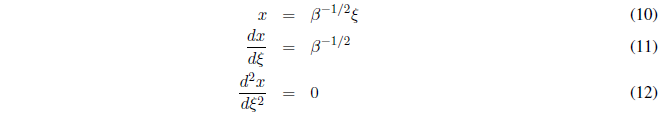
Substituting (11) and (12) in (9) and solving for \(\frac{d^2\Psi}{dx^2}\):
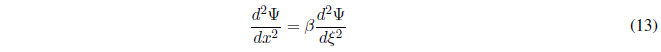
Substituting (10) and (13) in (6):
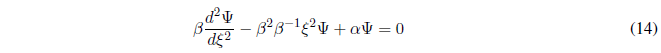
Dividing (14) by \(\beta\):
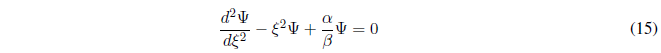
By taking a common factor from the wave function, the Hermite-Gauss equation is obtained, known in Mathematics even before the birth of quantum mechanics.