Quantum Theory
- Details
- Written by: Germán Fernández
- Category: Quantum theory
- Hits: 432
At the end of the 19th century, classical physics was capable of explaining almost all known physical phenomena. However, phenomena such as black body radiation, the photoelectric effect, atomic spectra, or the Compton effect did not have a satisfactory explanation.
The reason why classical physics is unable to explain such phenomena is because it is not an adequate theory to describe phenomena at the atomic level. In these dimensions a new theory is required, developed during the first quarter of the 20th century, called the quantum theory.
- Details
- Written by: Germán Fernández
- Category: Quantum theory
- Hits: 437
- Details
- Written by: Germán Fernández
- Category: Quantum theory
- Hits: 405
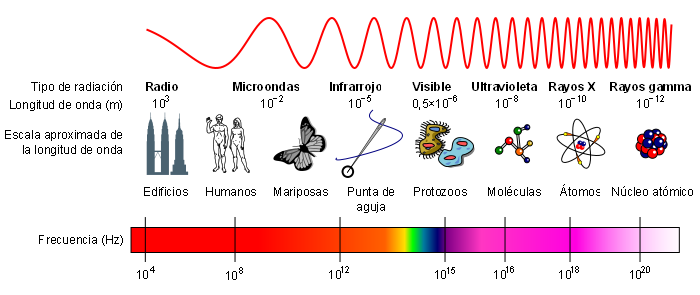
The electromagnetic spectrum is called the energy distribution of the set of electromagnetic waves.
The electromagnetic spectrum extends from radiation of shorter wavelengths, such as gamma rays and X-rays, through ultraviolet light, visible light and infrared rays, to electromagnetic waves of longer wavelengths, such as radio waves. The limit for the smallest possible wavelength is believed to be the Planck length while the maximum limit would be the size of the Universe.
- Details
- Written by: Germán Fernández
- Category: Quantum theory
- Hits: 414
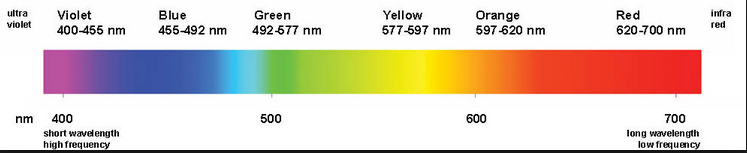
When a beam of white light passes through a prism, the different wavelengths that make it up are refracted differently, dispersing the light into a band of colors that correspond to all the wavelengths that make it up.
Higher frequency radiation (violet) is refracted more than lower frequency radiation (red), giving rise to the separation of light into the different radiations that compose it, called the spectrum of visible light.
- Details
- Written by: Germán Fernández
- Category: Quantum theory
- Hits: 487
When we break down sunlight using a prism we obtain a continuous spectrum, made up of a large number of wavelengths.
Gases, on the contrary, generate discontinuous or line spectra. The following figure shows the spectrum of helium, obtained by exciting the helium atoms by means of an electrical discharge, energy that they absorb to later emit it in the form of light.
The light emitted by the helium atoms when they are de-excited passes through a slit, is scattered in a prism and is recorded on photographic film.
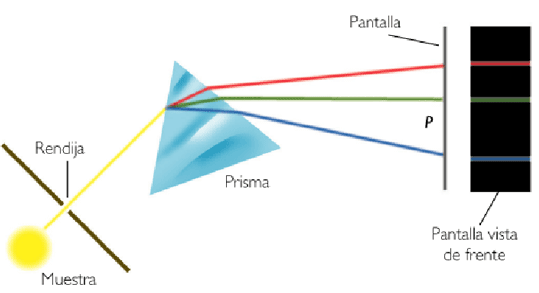
Each chemical element has a characteristic spectrum, which allows it to be identified. Thus, helium (from the Greek, helios, means sun) was discovered during a solar eclipse, 27 years before being isolated.
- Details
- Written by: Germán Fernández
- Category: Quantum theory
- Hits: 703
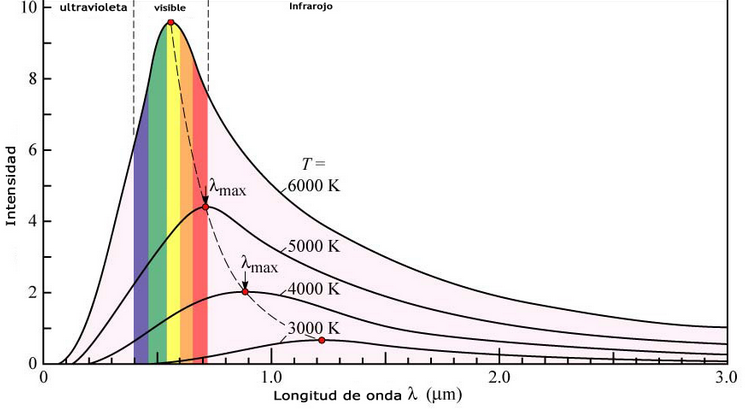
Another phenomenon that classical physics could not explain was the emission of radiation from a black body. A black body is an object capable of absorbing all the radiation that reaches it without reflecting anything. The intensity of the radiation emitted by a black body varies with the wavelength according to a characteristic curve that presents a maximum dependent on the temperature of the body. According to classical theory, the intensity of the radiation emitted by the black body must increase as the wavelength decreases, becoming infinite, a behavior that makes no physical sense.
- Details
- Written by: Germán Fernández
- Category: Quantum theory
- Hits: 516
In 1924, the Frenchman Victor de Broglie published his doctoral thesis, in which he developed the hypothesis that matter particles could exhibit wave behavior. De Broglie was inspired by Einstein's work on the photoelectric effect, in which light was made up of small corpuscles called photons, whose energy was $h\nu$. If a clearly wave-like phenomenon such as light had this corpuscular behavior, it might be possible for matter particles to have wave behavior.
Equating Einstein's equation, $E=mc^2$ to Planck's, $E=h\nu$:
$mc^2=h\nu$, replacing the frequency with $\nu=c/\lambda$:
$mc^2=h\frac{c}{\lambda}$, solving for the wavelength:
\begin{equation}\lambda=\frac{h}{mc}=\frac{h}{p}\end{equation}
Being p the quantity of movement or linear momentum of the particle.
This equation tells us that every particle that has momentum, photon, electron, proton, has an associated wave of length $\lambda$.
Read more: Wave-particle duality | Louis de Broglie hypothesis
- Details
- Written by: Germán Fernández
- Category: Quantum theory
- Hits: 472
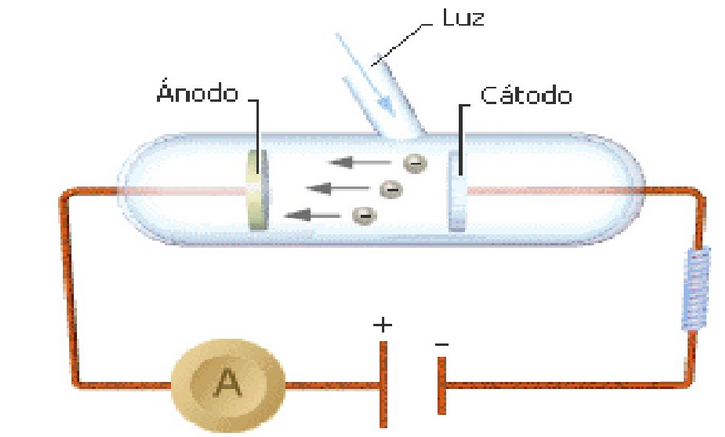
It is a physical phenomenon that consists of the emission of electrons by certain metals when a beam of light falls on its surface. It was observed in 1888 by Heinrich Hertz.
The photoelectric effect is characterized by:
- For the emission of electrons to occur, the incident light must have a minimum frequency, called the threshold frequency $\nu_0$
- The number of emitted electrons depends on the intensity of the incident radiation.
- The kinetic energy of electrons depends on the frequency of light.
- Details
- Written by: Germán Fernández
- Category: Quantum theory
- Hits: 509
Rutherford's atomic model, discussed in a previous section, does not explain how electrons are distributed in the atom. In addition, according to classical physics, a charged and moving particle -electrons- emits electromagnetic radiation, losing its energy and ending up falling on the nucleus.
The Bohr atomic model solves these problems based on Planck's hypothesis of the quantization of energy.
The Bohr model is based on the following postulates:
- The electron moves around the nucleus in circular orbits.
- The orbits allowed for the electron, in which it does not emit energy, are those in which the angular momentum takes values $n\hbar$, where n is an integer. The first orbit of the electron has n=1, the second n=2, etc.
- The electron passes from one orbit to another by absorbing or emitting quanta of energy.
- Details
- Written by: Germán Fernández
- Category: Quantum theory
- Hits: 490
In the classical world we can accurately measure the momentum and position of a particle. However, in the quantum world 
these magnitudes are affected by an uncertainty that prevents knowing their values simultaneously. Knowledge of the position of the particle produces a lack of knowledge of its momentum or velocity. Calling $\Delta x$ the uncertainty in the position and $\Delta p$ the uncertainty in its momentum, we can write the expression of the uncertainty principle as follows:
\begin{equation} \Delta x \cdot \Delta p\geq \frac{h}{4\pi} \end{equation}
- Details
- Written by: Germán Fernández
- Category: Quantum theory
- Hits: 411
In 1927, Erwin Schrödinger proposed that any electron or particle that possesses wave properties can be described by a function, represented by the Greek letter psi, $\psi$, called a wave function or state and contains all the information that is possible to know about that quantum system.
Schrödinger's equation, $\hat{H}\psi=E\psi$, is a differential equation whose solution gives us the wave function of the system and its energy. In this equation, $\hat{H}$, represents the Hamiltonian operator, whose expression for a one-dimensional system is:
\begin{equation} \hat{H}=-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}+V \end{equation}
where $\hbar=h/2\pi$ and V is the potential to which the particle is subjected.
The physical meaning of the wave function is given by its module squared, called probability density, $|\psi|^2$, and related to the probability of finding the particle in a given area of space.
- Details
- Written by: Germán Fernández
- Category: Quantum theory
- Hits: 437
It is a particle confined to the interval [0,a] on the x-axis. Within this interval the potential to which it is subjected is zero, while outside the interval it is infinite.
Solving the Schrödinger equation for this model gives us the wave function and energy.
\begin{equation} \psi_n=\sqrt\frac{2}{a}sin\frac{n\pi x}{a} \end{equation}
\begin{equation} E_n=\frac{h^2n^2}{8ma^2} \end{equation}
being n=1,2,3...., the number that quantizes the energy.
- Details
- Written by: Germán Fernández
- Category: Quantum theory
- Hits: 714
The solution of the Schrödinger equation for the hydrogen atom provides us with wave functions, called orbitals, and allowed energy levels. Given the symmetry of the problem, it is advisable to use spherical coordinates ($r,\theta,\varphi$). The set of hydrogenoid wave functions have the following form: \begin{equation} \psi_{nlm}(r,\theta,\varphi)=R_{nl}(r)Y_{lm}(\theta,\varphi) \end{equation}
The function $R_{nl}(r)$ is called the radial wavefunction and the function $Y_{lm}(\theta,\varphi)$ is known as the angular wavefunction and belongs to the family of spherical harmonics. n, l and m are the quantum numbers that arise from solving the Schrödinger equation and determine the type of orbital.
- n: principal quantum number , takes integer values, positive and different from zero. Represents the energy levels in the hydrogen atom. n=1,2,3...
- l: quantum number of the orbital angular momentum , takes values between 0 and n-1. l=0,1,2....
- m: magnetic quantum number, is associated with the z component of angular momentum and takes values between -l and +l. m=-l, -l+1,....0......l-1, l
- Details
- Written by: Germán Fernández
- Category: Quantum theory
- Hits: 508
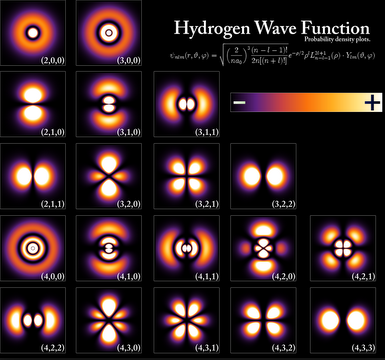
According to Born's interpretation, the squared module of the wave function gives us the probability density, the probability of finding the particle in certain coordinates. In this section we are going to represent the probability densities of the orbitals by surfaces that contain most of the probability of finding the electron.
Let us remember that the hydrogenoid wave functions are composed of the product of a radial part $R(r)$ by an angular part $Y(\theta,\varphi)$, called spherical harmonic. The radial part depends on the quantum numbers n and l, while the angular part depends on l and m.
To obtain the wave function of the ground state of the hydrogen atom we multiply the radial function $R(1s)=2(Z/a)^{3/2}e^{-Zr/a}$ by the spherical harmonic $Y_ {00}=1/\sqrt{4\pi}$:
\begin{equation} \psi_{1s}=\frac{1}{\sqrt{\pi}}\left(\frac{Z}{a}\right)^{3/2}e^{-Zr/ a} \end{equation}
In the case of the hydrogen atom Z=1, and the equation for the wave function remains:
\begin{equation} \psi_{1s}=\frac{1}{\sqrt{\pi}}\left(\frac{1}{a_0}\right)^{3/2}e^{-r/ a_0} \end{equation}
Squaring the wave function we obtain the probability density:
\begin{equation} \psi^2(1s)=\frac{1}{\pi a_0^3}e^{-2r/a_0} \end{equation}
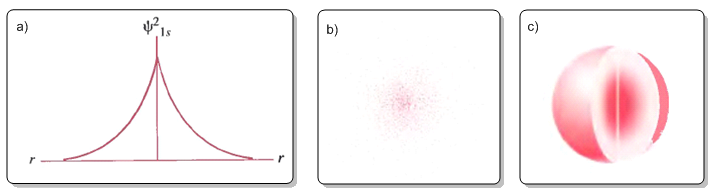
Figure (a) plots the electronic probability density $\psi^2$ against r. Figure (b) represents the probability density as a density of points. Figure (c) is the typical representation of the 1s orbital in which the area of space with a probability of finding the electron of 0.9 is delimited.
- Details
- Written by: Germán Fernández
- Category: Quantum theory
- Hits: 472
Spin is an intrinsic property of the electron that was initially associated with rotation, but since it does not depend on spatial coordinates it is independent of the state of motion of the particle. The value of the spin angular momentum is quantized, depending on a quantum number, $m_s$, which takes values +1/2 and -1/2.
The experimental demonstration of the existence of spin was carried out by Stern and Gerlach in 1920. By subjecting a beam of silver atoms, vaporized in an oven, to a variable magnetic field, they observed the splitting of the beam into two beams, due to the presence of an unpaired electron that in half of the silver atoms has $m_s=1/2$ and in the other half $m_s=-1/2$.
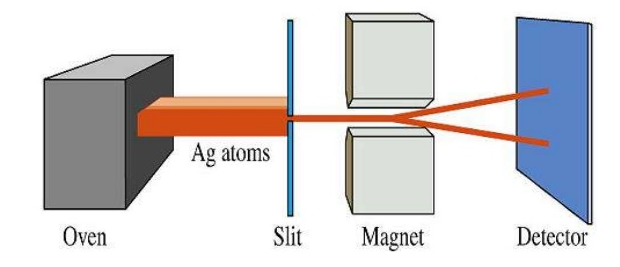
- Details
- Written by: Germán Fernández
- Category: Quantum theory
- Hits: 700
As we saw in previous sections, the energy levels of the hydrogen atom are given by the principal quantum number (n), being independent of the quantum numbers l and m. This situation changes in atoms with more than one electron due to the interaction between them. In polyelectronic atoms, the energy of the electron also depends on the quantum number l, with the electrons in the 2s subshell and those in the 2p being located at different energy levels. In the same way, the 3s, 3p and 3d have different energy.
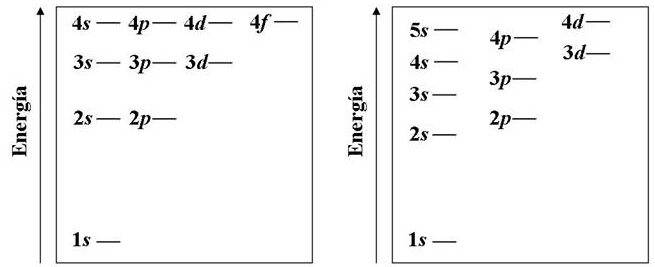
The diagram on the left represents the energy levels of hydrogen atoms (one electron). On the right we have the energy levels for a many electron atom.
- Details
- Written by: Germán Fernández
- Category: Quantum theory
- Hits: 513
The electronic configuration of an atom tells us how the electrons are distributed in the different layers, subshells and orbitals. This distribution is related to the physical properties of the elements. To write the electronic configuration of a polyelectronic atom we will use three rules: 1/ Filling or aufbau rule; 2/ Pauli exclusion principle; 3/ Hund's rule of maximum multiplicity.
- Rule of filling or aufbau. The electrons occupy the orbitals in such a way that the energy of the atom is minimized. That is, the lowest energy levels are occupied first. The order of filling the different sublayers is obtained by means of the following diagram in which we must start with the upper line and follow the arrows.
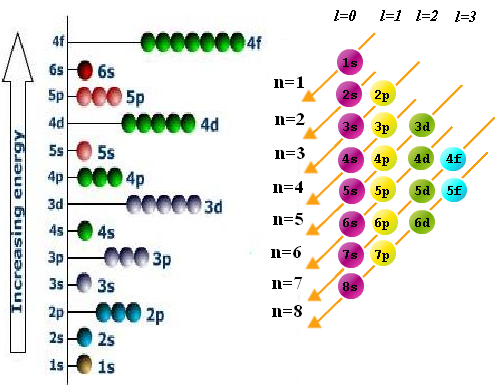
- Details
- Written by: Germán Fernández
- Category: Quantum theory
- Hits: 489
The inner electrons of the atom "block the view" (screen) of the nucleus to outer electrons, sensing a lower nuclear charge than the one that the nucleus actually has, called the effective nuclear charge $(Z_ef)$. To calculate the effective nuclear charge, we subtract the actual charge of the nucleus (atomic number, Z) from the shielding produced by the inner electrons (S). \begin{equation} Z_{ef}=ZS \end{equation} The electrons that are in innermost orbitals (penetrate further into the atom), with higher electron density in the vicinity of the nucleus shield external electrons more than electrons They are found in orbitals with an electron density farther from the nucleus. For example, the 1s orbital is the one with the greatest penetration of the atom, its electrons are very close to the nucleus and produce a significant shielding effect on external electrons. The next in order of penetration are the 2s, followed by the 2p...
Orbital penetration order: 1s>2s>2p>3s>3p>3d.
Read more: Effective Nuclear Charge, Shielding, and Slater's Rules
- Details
- Written by: Germán Fernández
- Category: Quantum theory
- Hits: 426