When we break down sunlight using a prism we obtain a continuous spectrum, made up of a large number of wavelengths.
Gases, on the contrary, generate discontinuous or line spectra. The following figure shows the spectrum of helium, obtained by exciting the helium atoms by means of an electrical discharge, energy that they absorb to later emit it in the form of light.

The light emitted by the helium atoms when they are de-excited passes through a slit, is scattered in a prism and is recorded on photographic film.
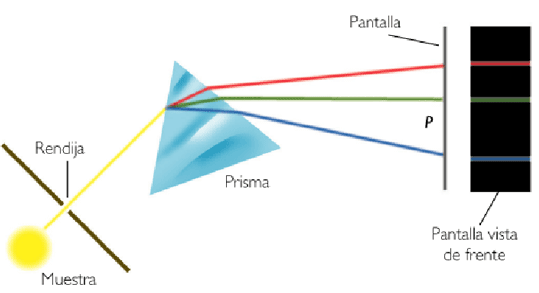
Each chemical element has a characteristic spectrum, which allows it to be identified. Thus, helium (from the Greek, helios, means sun) was discovered during a solar eclipse, 27 years before being isolated.
In 1885, Johamm Balmer, empirically obtained an equation that predicted the frequencies at which the spectral lines of the hydrogen atom appeared in the visible region (Balmer series).
\begin{equation} \nu=3.2881x10^{15}\ s^{-1}\left(\frac{1}{2^2}-\frac{1}{n^2}\right) \end{equation}
Where, $\nu$, is the frequency at which each spectrum line appears and $n$ is an integer greater than or equal to two.
Substituting in the equation n=3 the frequency of the red line is obtained, with n=4 the greenish blue one, with n=5 the blue one and so on.

Spectral lines give us important information about the structure of atoms, suggesting that electrons can only be found at certain energy levels. These experimental observations could not be explained by classical physics, giving rise to a new theory, quantum mechanics.
In 1888, Rydberg proposed a formula that generated the spectral lines both in the visible zone and in the infrared and ultraviolet.
\begin{equation}\nu=3.29x10^{15}\left(\frac{1}{n_i^2}-\frac{1}{n_f^2}\right)\end{equation}
Being $n_i$ and $n_f$ integers, with $n_i>n_f$
The Rydberg constant can be expressed in different units:
$R=1.096x10^{7}\;m^{-1}$
$R=3.29x10^{15}\;s^{-1}$
$R=2.18x10^{-18}\;J$



