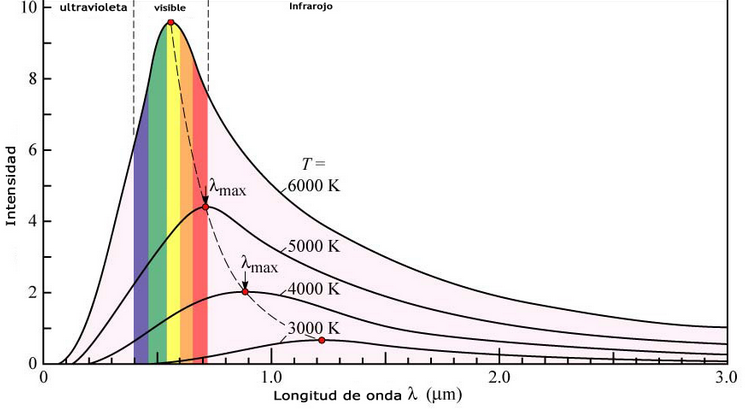
Another phenomenon that classical physics could not explain was the emission of radiation from a black body. A black body is an object capable of absorbing all the radiation that reaches it without reflecting anything. The intensity of the radiation emitted by a black body varies with the wavelength according to a characteristic curve that presents a maximum dependent on the temperature of the body. According to classical theory, the intensity of the radiation emitted by the black body must increase as the wavelength decreases, becoming infinite, a behavior that makes no physical sense.
Classical physics tries to predict these curves using the Rayleigh-Jeans equation:
$E(\lambda,T)=\frac{2ckT}{\lambda^4}$
This equation predicts well at long wavelengths but fails in the ultraviolet zone, since when the wavelength tends to zero the radiant energy tends to infinity. Problem known as the ultraviolet catastrophe.
The wavelength at which the curves reach their maximum depends on the temperature. Wien's Law predicts such a maximum:
$\lambda_{max}=\frac{0.0028976\;mK}{T}$
As can be seen, the maximum is reached at shorter wavelengths as the temperature increases.
The solution to this enigma came from Max Planck in 1900. To explain it, Planck must break with classical physics and assume that the black body emits radiation in the form of small packets, called energy quanta. The energy of one of these packages is given by the equation:
\begin{equation} E=h\nu \end{equation} where, $h=6.62607x10^{-34}\ Js$. Called Planck's equation.
Under this assumption, Planck arrives at an equation that perfectly describes the observed intensity curves.
\begin{equation}E(\nu,T)=\frac{8\pi h\nu^3}{c^2}\frac{1}{e^{h\nu/kT-1}}\end{equation}
Called Plack's Law.