According to Born's interpretation, the squared module of the wave function gives us the probability density, the probability of finding the particle in certain coordinates. In this section we are going to represent the probability densities of the orbitals by surfaces that contain most of the probability of finding the electron.
Let us remember that the hydrogenoid wave functions are composed of the product of a radial part $R(r)$ by an angular part $Y(\theta,\varphi)$, called spherical harmonic. The radial part depends on the quantum numbers n and l, while the angular part depends on l and m.
To obtain the wave function of the ground state of the hydrogen atom we multiply the radial function $R(1s)=2(Z/a)^{3/2}e^{-Zr/a}$ by the spherical harmonic $Y_ {00}=1/\sqrt{4\pi}$:
\begin{equation} \psi_{1s}=\frac{1}{\sqrt{\pi}}\left(\frac{Z}{a}\right)^{3/2}e^{-Zr/ a} \end{equation}
In the case of the hydrogen atom Z=1, and the equation for the wave function remains:
\begin{equation} \psi_{1s}=\frac{1}{\sqrt{\pi}}\left(\frac{1}{a_0}\right)^{3/2}e^{-r/ a_0} \end{equation}
Squaring the wave function we obtain the probability density:
\begin{equation} \psi^2(1s)=\frac{1}{\pi a_0^3}e^{-2r/a_0} \end{equation}
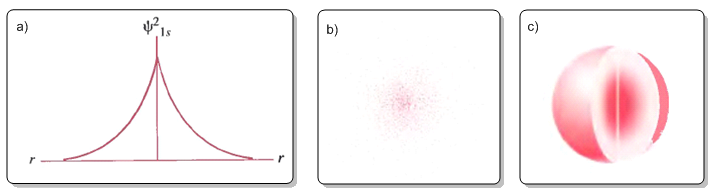
Figure (a) plots the electronic probability density $\psi^2$ against r. Figure (b) represents the probability density as a density of points. Figure (c) is the typical representation of the 1s orbital in which the area of space with a probability of finding the electron of 0.9 is delimited.
For the 2s orbital the radial function is given by the equation:
\begin{equation} R(2s)=\frac{1}{\sqrt{2}}\left(\frac{Z}{a}\right)^{3/2}\left(1-\frac{ Zr}{2a}\right)e^{-Zr/2a} \end{equation}
The angular part of the 2s orbital is still the harmonic $Y_{00}=\frac{1}{\sqrt{4\pi}}$. The product of both factors gives rise to the wavefunction of the 2s orbital.
\begin{equation} \psi(2s)=\frac{1}{\sqrt{\pi}}\left(\frac{Z}{2a}\right)^{3/2}\left(1-\ frac{Zr}{2a}\right)e^{-Zr/2a} \end{equation}
The square of this function gives us the probability density, which we can represent in different ways, just like we did with the 1s orbital.
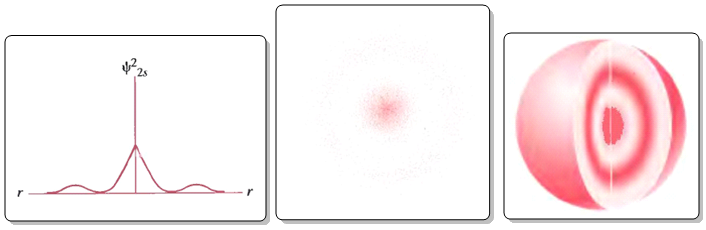
In the case of the 2s orbital we find a radial node (point of zero probability density) that is transferred to the orbital in the form of a spherical nodal surface. The number of radial nodes or spherical nodal surfaces is given by the expression: nl-1
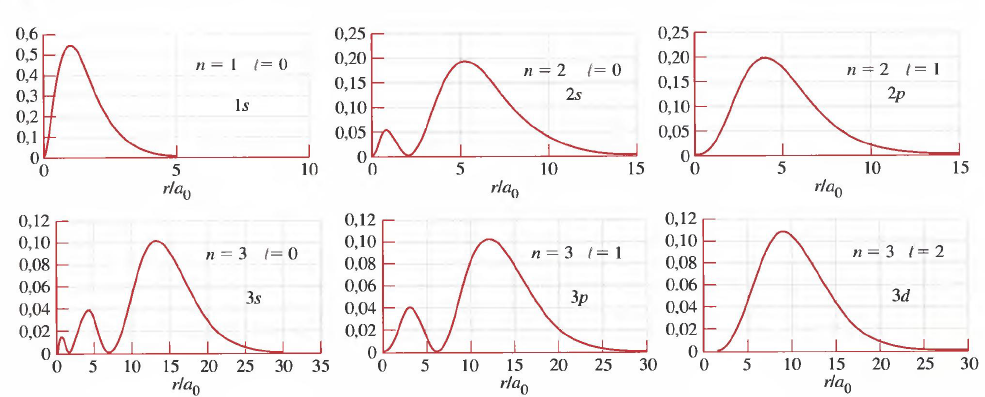
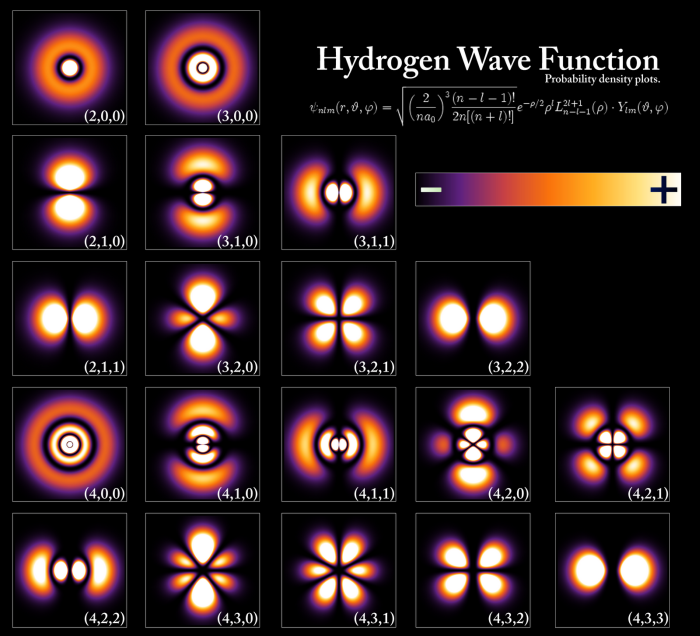
The following images show the radial probability densities, obtained by plotting $4\pi r^2R_{nl}^2$ against the radial coordinate (r), as well as the area of space with a very high probability of finding the electron. high (98%), known as orbital.