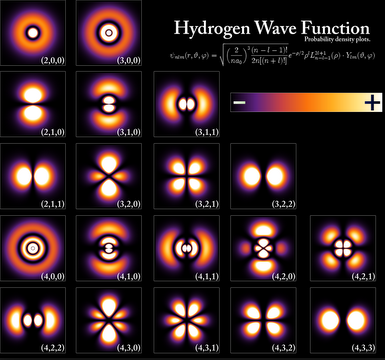
The solution of the Schrödinger equation for the hydrogen atom provides us with wave functions, called orbitals, and allowed energy levels. Given the symmetry of the problem, it is advisable to use spherical coordinates ($r,\theta,\varphi$). The set of hydrogenoid wave functions have the following form: \begin{equation} \psi_{nlm}(r,\theta,\varphi)=R_{nl}(r)Y_{lm}(\theta,\varphi) \end{equation}
The function $R_{nl}(r)$ is called the radial wavefunction and the function $Y_{lm}(\theta,\varphi)$ is known as the angular wavefunction and belongs to the family of spherical harmonics. n, l and m are the quantum numbers that arise from solving the Schrödinger equation and determine the type of orbital.
- n: principal quantum number , takes integer values, positive and different from zero. Represents the energy levels in the hydrogen atom. n=1,2,3...
- l: quantum number of the orbital angular momentum , takes values between 0 and n-1. l=0,1,2....
- m: magnetic quantum number, is associated with the z component of angular momentum and takes values between -l and +l. m=-l, -l+1,....0......l-1, l
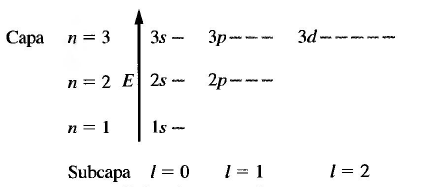
All orbitals with the same n form a shell or electronic level and have the same energy (degenerate). Orbitals with the same n but different l form a subshell or subshell. It is customary to represent the sublayers with letters, according to the notation: l=0 (s); 1=1(p); l=2(d); l=3(f).
The s subshells have a single orbital whose value of m=0.
The p subshells have three orbitals, one for each value that takes the quantum number m (-1,0,1).
The d subshells have 5 orbitals corresponding to the values of m (-2,-1,0,1,2).
The f subshells are made up of 7 orbitals.
The energy levels in which the orbitals of the hydrogen atom are arranged are given by the equation:
\begin{equation} E_n=-\frac{2.178x10^{-18}}{n^2}J \end{equation}
All orbitals located in the same shell (same value of n) have identical energy.
In the following image we can see the color maps that give us the areas of greatest electronic density and that outline the contour of the different hydrogenoid orbitals.