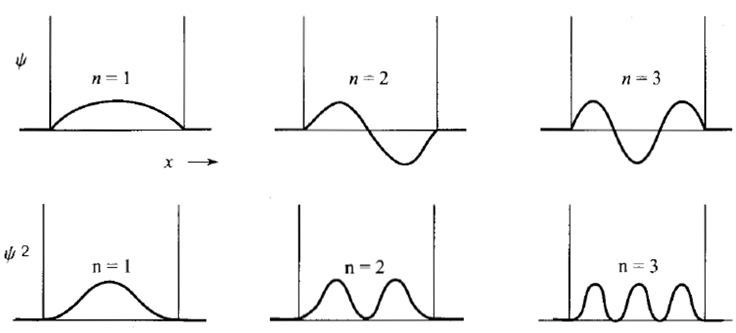
It is a particle confined to the interval [0,a] on the x-axis. Within this interval the potential to which it is subjected is zero, while outside the interval it is infinite.
Solving the Schrödinger equation for this model gives us the wave function and energy.
\begin{equation} \psi_n=\sqrt\frac{2}{a}sin\frac{n\pi x}{a} \end{equation}
\begin{equation} E_n=\frac{h^2n^2}{8ma^2} \end{equation}
being n=1,2,3...., the number that quantizes the energy.
The wave functions and their probability densities for the first three energy levels are shown in the following graphs.