Rutherford's atomic model, discussed in a previous section, does not explain how electrons are distributed in the atom. In addition, according to classical physics, a charged and moving particle -electrons- emits electromagnetic radiation, losing its energy and ending up falling on the nucleus.
The Bohr atomic model solves these problems based on Planck's hypothesis of the quantization of energy.
The Bohr model is based on the following postulates:
- The electron moves around the nucleus in circular orbits.
- The orbits allowed for the electron, in which it does not emit energy, are those in which the angular momentum takes values $n\hbar$, where n is an integer. The first orbit of the electron has n=1, the second n=2, etc.
- The electron passes from one orbit to another by absorbing or emitting quanta of energy.
Under these assumptions, the Bohr model allows the calculation of the energy of the electron and the radius of the different orbits that will depend on the quantum number n.
The allowed orbits (stationary states) have a radius that is given by:
\begin{equation} r_n=n^2a_0 \end{equation} where n=1,2,3,.... and $a_0=0.53\;Anstrong$
The energy of the electron is given by:
\begin{equation} E_n=-\frac{R_H}{n^2} \end{equation}
with $R_H=2.179x10^{-18}\ J$
The lowest energy state, n=1, is known as the ground state. By providing energy, the electron rises to higher levels n=2,3,4..... going to an excited state. When the electron returns from an excited state to the fundamental one, it emits light (photons) whose energy is equal to the energy difference between the final and initial orbits.
\begin{equation} \Delta E=E_f-E_i=\frac{-R_H}{n_f^2}-\frac{-R_H}{n_i^2}=R_H\left(\frac{1}{n_i^2 }-\frac{1}{n_f^2}\right) \end{equation} Where, $R_H=2.179x10^{-18}J$
This energy difference between levels is equal to the energy of the emitted or absorbed photon during the transition. Therefore, we can calculate the frequency of said photon with the Planck equation.
\begin{equation} \Delta E=h\nu \end{equation}
Example. Determine the wavelength of the Balmer series line for hydrogen corresponding to the transition from n=5 to n=2.
Steps to follow: (1) determine the energy difference between both levels; (2) equate this energy difference to $h\nu$ (energy of the emitted photon; (3) obtain the wavelength with the relation $\lambda=c/\nu$.
\begin{equation} \Delta E=2.179x10^{-18}J\left(\frac{1}{5^2}-\frac{1}{2^2}\right)=-4.567x10^{ -19}J \end{equation}
The minus sign indicates that it is emitted energy, since the electron passes from a higher orbit to a lower one.
\begin{equation} \nu=\frac{\Delta E}{h}=\frac{4.576x10^{-19}J}{6.626x10^{-34}Js}=6.906x10^{14}s^ {-1} \end{equation}
\begin{equation} \lambda=\frac{c}{\nu}=\frac{2.998x10^8\ m/s}{6.906x10^{14}\ s^{-1}}=4.341x10^{ -7}\ m \end{equation}
As we can see in this example, the Bohr model allows us to predict the spectral lines of the hydrogen atom. After being excited, the hydrogen atom decays, emitting light with a frequency predictable by this model. However, the Bohr model fails when applied to atoms with more than one electron.
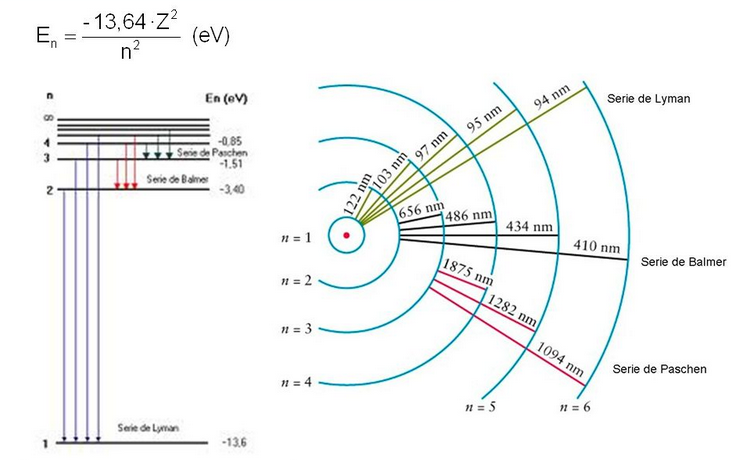
Another achievement of Bohr's theory is the prediction of the ionization energy of the hydrogen atom that can be generalized to any single-electron atom. The ionization of the atom consists in the passage of the electron from the fundamental state $(n_i=1)$ to the continuum $(n_f=\infty)$
\begin{equation} \Delta E=R_H\left(\frac{1}{1^2}-\frac{1}{\infty}\right)=R_H \end{equation}
The Bohr model also works with hydrogenoid atom, which are those that have only one electron, although their nucleus is formed by more than one proton ($He^+, Li^{2+}$). In this case the energy of the levels is given by:
\begin{equation} E_n=-\frac{Z^2R_H}{n^2} \end{equation}
Example. Determine the wavelength of the light emitted in the electronic transition from n=5 to an=3 in the $Be^{3+}$
Subtracting the energy of the final level minus that of the initial one, we obtain:
\begin{equation} \Delta E=Z^2R_H\left(\frac{1}{n_i^2}-\frac{1}{n_f^2}\right)=4^2\cdot 2.179x10^{- 18}J\left(\frac{1}{5^2}-\frac{1}{3^2}\right)=-2.479x10^{-18}\ J \end{equation}
According to Planck's equation $\Delta E=h\nu$ and since $\nu=c/\lambda$, we can write $\lambda=hc/\Delta E$. From which we get $\lambda=8.013x10^{-8}\ m$.



