The differential equation (16) has a solution of the type:
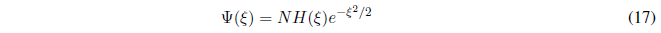
We calculate the first and second derivatives of (17):
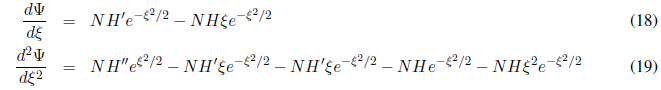
Substituting (17) and (19) in (16) and simplifying
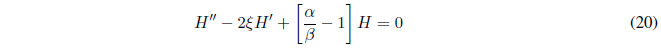
Equation (20) is known as the Hermite differential equation. H is a polynomial function, known as a Hermite polynomial.
The Hermite polynomial has the following form:
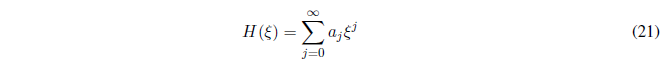
Deriving (21)
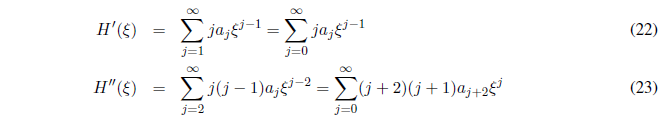
Substituting equations (21), (22) and (23) in (20):
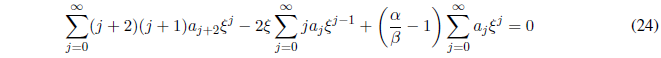
Grouping all the terms in a summation and taking out a common factor:
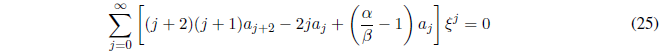
For equation (25) to be true, the terms enclosed in brackets must be null
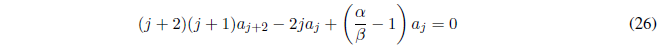
Solving for \(a_{j+2}\) we obtain the recurrence relation.
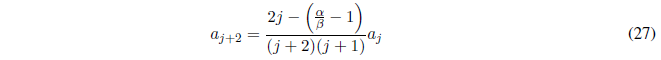
Once the coefficients \(a_0\) and \(a_1\) of the Hermite polynomial are known, the rest of the coefficients can be calculated using the recurrence law.
For the wave function to be valid in Quantum Mechanics, it must be quadratically integrable, that is, normalizable.
The Hermite polynomial is an expansion with infinite terms and increases faster than the exponential decreases, making the wave function approach infinity as x approaches plus infinity and minus infinity.
In order for the wave function to be quadratically integrable, it is necessary to truncate the polynomial for a value of \(j=v\), so that \(a_v\) is the last non-zero coefficient of the development.
Making \(j=v\) in the recurrence law, gives us:
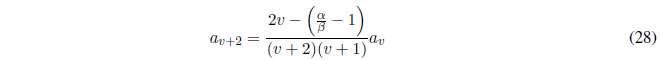
Since \(a_v\) is the last nonzero term and \(a_{v+2}=0\), equation (28) will hold only if the numerator of the quotient is zero.
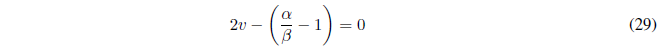
Substituting \(\alpha\) and \(\beta\) for their value
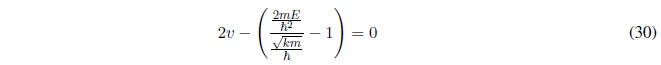
Solving E in (30) we are left with:
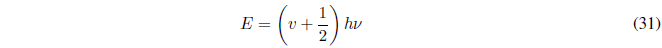
Where \(\nu\) represents the frequency of the oscillator and v is the quantum number that takes values 0,1,2,3,.....
Characteristics of the one-dimensional harmonic oscillator
- The energy of the harmonic oscillator is quantized according to the quantum number v=1,2,3,....
- The state v=0, is the one with the lowest energy (fundamental state)
- The energy levels of the harmonic oscillator are equally spaced. As v increases by one unit, the energy increases by \(h\nu\)



