Solvent (A) \begin{equation} \mu_A=\mu_{A}^{0}+RTlnx_A \end{equation} To define the normal state we must cancel the term $RTlnx_A$ and for this we do $x_A \rightarrow 1$ so that $lnx_A \rightarrow 0$ \begin{equation} \mu_{A}^{0}=\mu_{A}^{\ast}(T,P) \end{equation} The normal state of the solvent is defined as a pure solvent at the temperature and pressure of the solution.
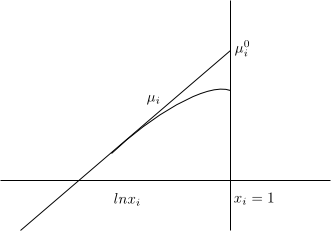
Solute (i) \begin{equation} \mu_i=\mu_{i}^{0}+RTlnx_i \end{equation} To define the normal state we must make $x_i \rightarrow 1$, but when $x_i$ increases the solution is no longer ideally dilute. This forces us to define the normal state $\mu_{i}^{0}$ in a fictitious way.
$µ_i^{0}$ is defined as the state in which i is pure and also each molecule of i experiences the same intermolecular forces as in an ideal dilute solution.