It allows to determine the steady laminar flow (dV/dt) for an incompressible fluid, of constant viscosity, through a cylindrical tube of radius r.
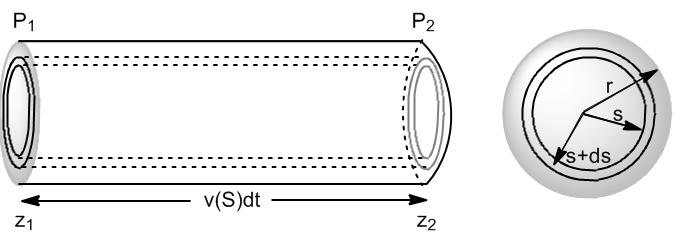
Let us consider a fluid flowing through a cylindrical pipe of radius r. Let us take an infinitesimal element of length z and internal radius s, with a pressure $p_1$ at the input and $p_2$ at the output.

We are going to write the forces that act on the fluid layer situated between s and s+ds.
- Hydrostatic pressure forces $(F=PS)$
- Force due to inlet pressure: $F_1=2\pi SdS\cdot P_1$
- Force due to outlet pressure: $F_2=-2\pi SdS\cdot P_2$
- friction forces.
- Friction with the inner part $F_{RI}=-\eta\cdot 2\pi Sdz(dV/dS)_s$. Since the velocity gradient is negative, the friction force is positive since the internal layers go faster and accelerate the fluid layer considered.
- Friction with the outer wall $F_{RE}=\eta\cdot 2\pi (S+dS)dz(dV/dS)_{S+dS}$. This friction force is negative since it opposes the movement of the considered layer.
Once the stationary regime is reached: $\sum\vec{F_i}=0$
\begin{equation} 2\pi SdS\cdot P_1-2\pi SdS\cdot P_2-\eta2\pi Sdz(dv/dS)_S+\eta 2\pi (S+dS)dz(dV/dS)_{ S+dS}=0 \end{equation}
Since $P_2=P_1+dP$
\begin{equation} 2\pi SdS\cdot P_1-2\pi SdS(P_1+dP)-\eta2\pi Sdz(dv /dS)_S+\eta 2\pi (S+dS)dz(dV/dS)_{S+dS}=0 \end{equation}
Simplifying the previous expression
\begin{equation} -\cancel{2\pi} SdSdP+ \cancel{2\pi}\eta dz\left[(S+dS)(dv/dS)_{S+dS}-S(dv/dS)_s\right]=0 \end{equation}
Taking into account Consider the definition of derivative: $df(x)=f(x+dx)-f(x)$, we can write the previous expression in the following form \begin{equation} -SdSdP+\eta dzd\left[s\frac {dv}{dS}\right]=0 \end{equation}
\begin{equation} \frac{dP}{dz}SdS=\eta d\left[s\frac{dv}{dS}\right] \end{equation}
Integrating with the constant pressure gradient
\begin{equation} \frac{dP}{dz}\frac{S^2}{2}=\eta S\frac{dv}{dS} + C \end{equation}
Since dv/ds cannot be infinite, if S=0
\begin{equation} 0=0+C \; \rightarrow \;C=0 \end{equation}
Solving for dv
\begin{equation} dv=\frac{1}{2\eta}\frac{dP}{dz}SdS \end{equation}
Integrating again
\begin{equation} v(S)=\frac{1}{2\eta}\frac{dP}{dz}\frac{s^2}{2}+C \end{equation}
We calculate the new constant of integration, C, knowing that in the pipe walls the flow is zero, $v(S=r)=0$
\begin{equation} 0=\frac{1}{2\eta}\frac{dP}{dz} \frac{r^2}{2}+C \;\rightarrow C=-\frac{1}{4\eta}\frac{dP}{dz}r^2 \end{equation}
Substituting the constant of integration in the velocity equation v(s)
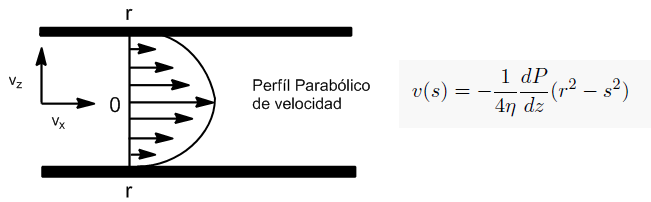
\begin{equation} v(s)=-\frac{1}{4\eta}\frac{dP}{dz}(r^2-s^2) \end{equation}
Equation that gives us a parabolic profile for the velocity of a fluid in steady state.
In one dt the volume of fluid that has moved through the crown of thickness ds is: $dV=2\pi SdS\cdot v(s)dt$. The total volume that circulates through the conduction is obtained by integrating from S=0 to S=r.
\begin{equation} \frac{dV}{dt}=\int_{0}^{r}2\pi S\cdot v(S)dS \end{equation}
Substituting v(S) for its value:
\begin{equation} \frac{dV}{dt}=2\pi \int_{0}^{r}S\frac{-1}{4\eta}(r^2-s^2)\frac{dP} {dz}=\frac{-\pi}{2\eta}\frac{dP}{dz}\left[\frac{r^4}{2}-\frac{r^4}{4}\right ] \end{equation}
Making the difference and simplifying gives the Poiseuille differential equation.
\begin{equation} \frac{dV}{dt}=\frac{-\pi r^4}{8\eta}\frac{dP}{dz} \end{equation}
In the case of liquids we can integrate since they are not very compressible and the volume is independent of pressure.
\begin{equation} \frac{\Delta V}{\Delta t}=\frac{-\pi r^4}{8\eta}\frac{\Delta P}{\Delta z} \end{equation}



