The deduction is analogous to thermal conductivity or viscosity with the difference that matter is transported.
The net flux of matter (in moles) through the $z_0$ plane is given by:
\begin{equation} J_z=J_{\uparrow}-J_{\downarrow}=\frac{dN_{\uparrow}}{N_A }-\frac{dN_{\downarrow}}{N_A} \end{equation}
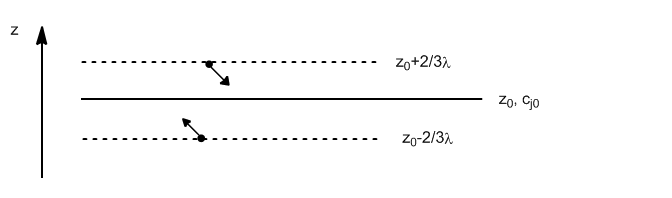
The number of molecules passing through $z_0$ from below is given by:
\begin{equation} dN_{\uparrow}=\frac{1} {4}\bar{v}\frac{N_{\uparrow}}{V}\frac{N_A}{N_A}=\frac{1}{4}\bar{v}N_A\frac{c_{\uparrow }}{V} \end{equation}
Substituting $c_{\uparrow}$ for the concentration of molecules in the plane $z_0-2/3\lambda$
\begin{equation} dN_{\uparrow}=\frac{1 }{4}\bar{v}N_A\left[c_{j0}-\frac{2}{3}\lambda\left(\frac{dc_j}{dz}\right)_0\right] \end{equation}
Analogously we write the number of molecules that cross $z_0$ from above.
\begin{equation} dN_{\downarrow}=\frac{1}{4}\bar{v}N_A\left[c_{j0}+\frac{2}{3}\lambda\left(\frac{dc_j }{dz}\right)_0\right] \end{equation}
Substituting in $J_z$
\begin{equation} J_z=\frac{1}{4}\bar{v}\frac{-4}{3} \lambda\frac{dc_j}{dz}\frac{-1}{3}\bar{v}\lambda\frac{dc_j}{dz} \end{equation}
From which it follows that the diffusion coefficient is given by:
\begin{equation} D=\frac{1}{3}\bar{v}\lambda \end{equation}
A rigorous treatment gives us:
\begin{equation} D=\frac{3\pi}{ 16}\lambda \bar{v} \end{equation}
Substituting $\lambda=\frac{1}{\sqrt{2}\pi d^2}\frac{kT}{P}$ and $\bar{ v}=\left(\frac{8kT}{\pi m}\right)^{1/2}$, we are left with:
\begin{equation} D=\frac{8}{8d^2}\left( \frac{kT}{\pi m}\right)^{1/2}\frac{kT}{P} \end{equation}



