Diffusion: Fick's First Law} If $c_{j,1}\neq c_{j,2}$ and $c_{k,1}\neq c_{k,2}$, removing the partition produces a movement of the species j,k that will reduce or eliminate the difference in concentrations between the two containers.
Diffusion is a macroscopic movement of the components of a system due to concentration differences. If $c_{j,1}$ is less than $c_{j,2}$, there is a net flux of j from 2 to 1 until concentrations and chemical potentials of j and k equalize throughout the cell.
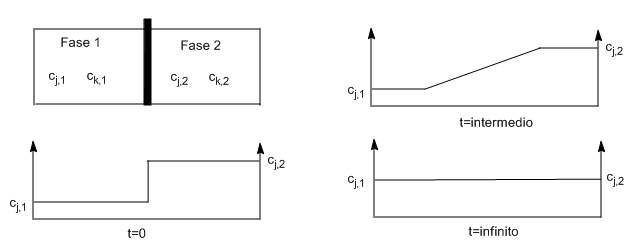
In diffusion all molecules have random speeds. However, since the concentration on the right side of a perpendicular plane is higher than on the left side, molecules of j are more likely to cross from right to left of the plane than from left to right, producing a net flux of j toward the left.
Fick's First Law gives us the speed of diffusion. \begin{equation} \frac{dn_j}{dt}=D_{jk}A\frac{dc_j}{dz} \end{equation} \begin{equation} \frac{dn_k}{dt}=D_{kj} A\frac{dc_k}{dz} \end{equation} $\frac{dn_j}{dt}$, represents the flow velocity of j (moles/s) through the plane P of area A, perpendicular to the z axis , where $\frac{c_j}{dz}$ is the concentration gradient in said plane.
$D_{jk}$, is a constant of proportionality called the diffusion coefficient. $D_{jk}$, depends on T,P and local composition, varying significantly with distance and with time throughout the diffusion cell.



