Substance in contact with deposits at different temperatures will eventually reach a steady state in which there will be a uniform temperature gradient dT/dz.
The heat flux dq/dt (measured in J/s) through any plane perpendicular to z is proportional to the cross-sectional area and the temperature gradient.
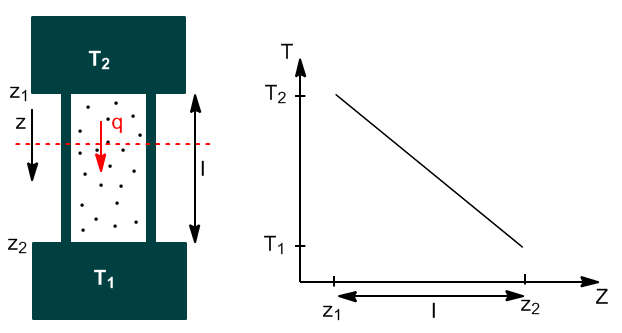
The mathematical expression that relates these physical magnitudes is known as Fourier's Law of thermal coduction.
\begin{equation} \frac{dq}{dt}=-kA\frac{dT}{dz} \end{equation}
Being k a constant of proportionality, called thermal conductivity of the substance, whose units are: $J/K\;cm\;s$. Good thermal conductors have high constants $k(Cu(s))=10 J/Kcms$. Bad thermal conductors have small constants $k(CO_2(g))=10^{-4}J/Kcms$
The constant k depends on temperature and pressure for pure substances, in the case of mixtures it also depends on the composition. In gases it increases with temperature.
Fourier's Law can also be written in terms of heat flux per unit time and area: J. Called heat flux density, whose units are $J/m^2s$
\begin{equation} J=\frac{1}{A}\frac{dq}{dt}=-k\frac{dT}{dx} \end{equation}
Heat transfer in gases takes place by molecular collisions. Higher temperature molecules have higher energy and in collisions give up part of this energy to lower temperature molecules. Since gas molecules have great freedom of movement, heat transmission usually also occurs by convection, due to the movement of the fluid. Another way of transmitting heat is radiation, due to the emission of electromagnetic waves by hot bodies that are absorbed by cold ones.
For Fourier's Law to be applicable, three conditions must be met:
- Isotropic system (all directions are the same)
- Small temperature gradient.
- There is no heat transfer by conduction or radiation.



