Two heat reservoirs with respective temperatures of 325 and 275 K are brought into contact by an iron rod 200 cm long and 24 cm^2 in cross section. Calculate the heat flux between the reservoirs when the system reaches its steady state. The thermal conductivity of iron at 25ºC is 0.804 J/Kcms.
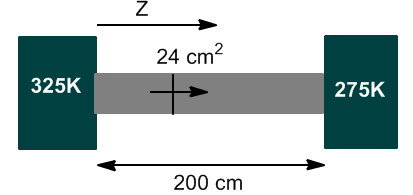
The system is in steady state and has a constant temperature gradient which is given by:
\begin{equation} \frac{dT}{dz}=\frac{\Delta T}{\Delta z}=\frac{275-325}{200}=-0.25K/cm \end{equation}
The heat flow through a cross section of the conductor is given by Fourier's Law:
\begin{equation} \frac{dq}{dt}=-kA\frac{dT}{dz}=-0804\;J/Kcms\cdot 24\;cm^2\cdot(-0.25K/cm)= 4.824\;J/s \end{equation}



