The kinetic theory of gases gives theoretical expressions for thermal conductivity with results consistent with experience. We start from the following approximations:
- Molecules are rigid spheres of diameter d.
- Molecules move at average velocity $\left(\frac{8RT}{\pi M}\right)^{1/2}$
- The average distance traveled by a molecule between two collisions is: $\lambda=\frac{1}{\sqrt{2}\pi d^2}\frac{kT}{P}$
- In each collision the molecular properties adjust to those of that position.
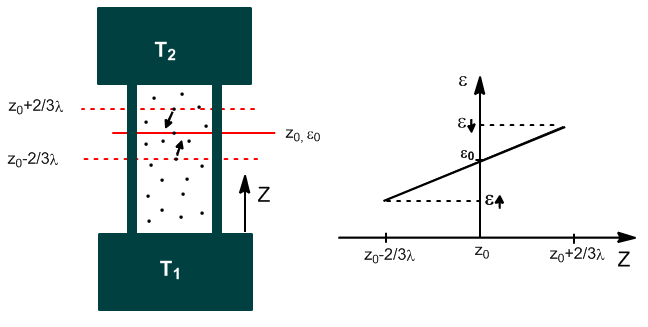
To calculate k, we must obtain the net flow of heat per unit time and area through the plane $z_0$
\begin{equation} J_z=J_{\uparrow}-J_{\downarrow}=\epsilon_{\uparrow}dN_{\uparrow}-\epsilon_{\downarrow}dN_{\downarrow} \end{equation}
Where, $dN_{\uparrow}$, represents the number of molecules traversing $z_0$ from above per unit area in one dt.
Where, $dN_{\downarrow}$, represents the number of molecules traversing $z_0$ from below per unit area in one dt.
$\epsilon_{\uparrow}$ and $\epsilon_{\downarrow}$ represent the average energy of each of those molecules.
Since there is no convection $dN_{\uparrow}=dN_{\downarrow}$.
We calculate $dN_{\uparrow}$ considering the plane $z_0$ as a wall of area A on which the molecules collide. The number of collisions in a dt will be given by:
$dN_{\uparrow}=dN_{\downarrow}=\frac{1}{4}\bar{v}\frac{N}{V}$
Substituting in the expression for the heat flux
$J_z=\frac{1}{4}\bar{v}\frac{N}{V}(\epsilon_{\uparrow}-\epsilon_{\downarrow})$
The energy of the molecules that cross $z_0$ is the one they acquire during the last collision, which on average occurs at $z_0\pm 2/3\lambda$.
$\epsilon_{\uparrow}$: is the energy possessed by the molecule in $z_0-2/3\lambda$.
$\epsilon_{\downarrow}$: is the energy possessed by the molecule in $z_0+2/3\lambda$.
Assuming a linear variation of energy with z, in the vicinity of $z_0$, we can write:
\begin{equation} \epsilon_{\uparrow}=\epsilon(z_0-2/3\lambda)=\epsilon_0-\left(\frac{\partial\epsilon}{\partial z}\right)_0\cdot 2 /3\lambda \end{equation}
\begin{equation} \epsilon_{\downarrow}=\epsilon(z_0+2/3\lambda)=\epsilon_0+\left(\frac{\partial\epsilon}{\partial z}\right)_0\cdot 2/ 3\lambda \end{equation}
Substituting the average energies of the molecules that cross $z_0$ into the net heat flux:
\begin{equation} J_z=\frac{1}{4}\bar{v}\frac{N}{V}\left[\epsilon_0-2/3\lambda\left(\frac{\partial\epsilon} {\partial z}\right)_0-\epsilon_0-2/3\lambda\left(\frac{\partial\epsilon}{\partial z}\right)_0\right]=\frac{1}{4} \bar{v}\frac{N}{V}\left[\frac{-4}{3}\lambda\left(\frac{\partial\epsilon}{\partial z}\right)_0\right] \end{equation}
Simplifying we are left with:
\begin{equation} J_z=-\frac{1}{3}\bar{v}\frac{N}{V}\lambda\left(\frac{\partial\epsilon}{\partial z}\right) _0 \end{equation}
The energy, $\epsilon$, of a molecule depends on the temperature and this in turn depends on z. Applying the chain rule:
\begin{equation} \frac{\partial\epsilon}{\partial z}=\frac{\partial\epsilon}{\partial T}\frac{dT}{dz}=\frac {\partial U_m/N_A}{\partial T}\cdot\frac{dT}{dz}=\frac{C_{vm}}{N_A}\frac{dT}{dz} \end{equation}
Where taken into account that: $C_{vm}=dU_m/dT$
Substituting into the heat flux density $J_z$:
\begin{equation} J_z=-\frac{1}{3}\frac{N}{V}\bar{v}\lambda\frac{C_{vm} }{N_A}\frac{dT}{dz} \end{equation}
Obtaining for the thermal conductivity the value:
\begin{equation} k=\frac{1}{3}\frac{N}{V}\bar {v}\lambda\frac{C_{vm}}{N_A} \end{equation}
Equation in which the ratio N/V is usually replaced by $\rho$ (density of molecules per unit volume)
\begin{ equation} k=\frac{1}{3}\rho \bar{v}\lambda\frac{C_{vm}}{N_A} \end{equation}
There are more rigorous developments, assuming that the molecules follow the distribution of Maxwell velocities instead of mean velocity: \begin{equation} k=\frac{25\pi}{64}\lambda\bar{v}\rho\frac{C_{vm}}{N_A} \end{equation}
Equation that is more manageable if we make the following substitutions: $\lambda=\frac{1}{\sqrt{2}\pi d^2}\frac{kT}{P}$; $\rho=\frac{N}{V}=\frac{P}{RT}$ and $\bar{v}=\left(\frac{8kT}{\pi m}\right)^{1/ 2}$:
\begin{equation} k=\frac{25}{32}\left(\frac{RT}{\pi M}\right)^{1/2}\frac{1}{N_Ad^2 }C_{vm} \end{equation}



