La teoría cinética de los gases da expresiones teóricas para la conductividad térmica con resultados acordes con la experiencia. Partimos de las siguientes aproximaciones:
- Las moléculas son esferas rígidas de diámetro d.
- Las moléculas se mueven al velocidad media $\left(\frac{8RT}{\pi M}\right)^{1/2}$
- La distancia media recorrida por una molécula entre dos colisiones es: $\lambda=\frac{1}{\sqrt{2}\pi d^2}\frac{kT}{P}$
- En cada colisión las propiedades moleculares se ajustan a las de esa posición.
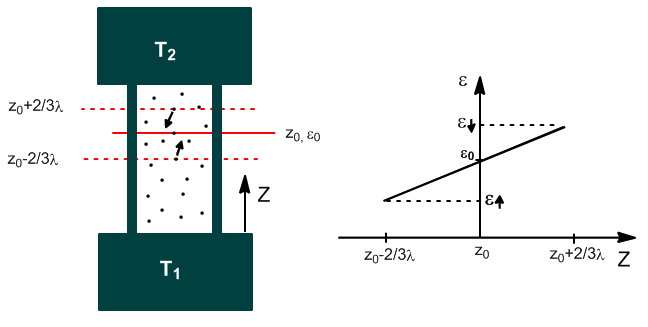
Para calcula k, debemos obtener el flujo neto de calor por unidad de tiempo y área a través del plano $z_0$
\begin{equation} J_z=J_{\uparrow}-J_{\downarrow}=\epsilon_{\uparrow}dN_{\uparrow}-\epsilon_{\downarrow}dN_{\downarrow} \end{equation}
Donde, $dN_{\uparrow}$, representa el número de moléculas que atraviesan $z_0$ desde arriba por unidad de área en un dt.
Donde, $dN_{\downarrow}$, representa el número de moléculas que atraviesan $z_0$ desde abajo por unidad de área en un dt.
$\epsilon_{\uparrow}$ y $\epsilon_{\downarrow}$ representan la energía media de cada una de esas moléculas.
Al no existir convección $dN_{\uparrow}=dN_{\downarrow}$.
Calculamos $dN_{\uparrow}$ considerando el plano $z_0$ como una pared de área A sobre la que chocan las moléculas. El número de colisiones en un dt vendrá dado por:
$dN_{\uparrow}=dN_{\downarrow}=\frac{1}{4}\bar{v}\frac{N}{V}$
Sustituyendo en la expresión del flujo de calor
$J_z=\frac{1}{4}\bar{v}\frac{N}{V}(\epsilon_{\uparrow}-\epsilon_{\downarrow})$
La energía de las moléculas que cruzan $z_0$ es la que adquieren durante la última colisión, que de media se produce en $z_0\pm 2/3\lambda$.
$\epsilon_{\uparrow}$: es la energía que posee la molécula en $z_0-2/3\lambda$.
$\epsilon_{\downarrow}$: es la energía que posee la molécula en $z_0+2/3\lambda$.
Suponiendo una variación lineal de la energía con z, en las proximidades de $z_0$, podemos escribir:
\begin{equation} \epsilon_{\uparrow}=\epsilon(z_0-2/3\lambda)=\epsilon_0-\left(\frac{\partial\epsilon}{\partial z}\right)_0\cdot 2/3\lambda \end{equation}
\begin{equation} \epsilon_{\downarrow}=\epsilon(z_0+2/3\lambda)=\epsilon_0+\left(\frac{\partial\epsilon}{\partial z}\right)_0\cdot 2/3\lambda \end{equation}
Sustituyendo las energías medias de las moléculas que cruzan $z_0$ en el flujo neto de calor:
\begin{equation} J_z=\frac{1}{4}\bar{v}\frac{N}{V}\left[\epsilon_0-2/3\lambda\left(\frac{\partial\epsilon}{\partial z}\right)_0-\epsilon_0-2/3\lambda\left(\frac{\partial\epsilon}{\partial z}\right)_0\right]=\frac{1}{4}\bar{v}\frac{N}{V}\left[\frac{-4}{3}\lambda\left(\frac{\partial\epsilon}{\partial z}\right)_0\right] \end{equation}
Simplificando nos queda:
\begin{equation} J_z=-\frac{1}{3}\bar{v}\frac{N}{V}\lambda\left(\frac{\partial\epsilon}{\partial z}\right)_0 \end{equation}
La energía, $\epsilon$, de una molécula depende de la temperatura y ésta a su vez depende de z. Aplicando la regla de la cadena: \begin{equation} \frac{\partial\epsilon}{\partial z}=\frac{\partial\epsilon}{\partial T}\frac{dT}{dz}=\frac{\partial U_m/N_A}{\partial T}\cdot\frac{dT}{dz}=\frac{C_{vm}}{N_A}\frac{dT}{dz} \end{equation} Donde se ha tenido en cuenta que: $C_{vm}=dU_m/dT$
Sustituyendo en la densidad de flujo de calor $J_z$: \begin{equation} J_z=-\frac{1}{3}\frac{N}{V}\bar{v}\lambda\frac{C_{vm}}{N_A}\frac{dT}{dz} \end{equation} Obteniéndose para la conductividad térmica el valor: \begin{equation} k=\frac{1}{3}\frac{N}{V}\bar{v}\lambda\frac{C_{vm}}{N_A} \end{equation} Ecuación en la que habitalmente se reempla el cociente N/V por $\rho$ (densidad de moléculas por unidad de volumen) \begin{equation} k=\frac{1}{3}\rho \bar{v}\lambda\frac{C_{vm}}{N_A} \end{equation} Existen desarrollos más rigurosos, suponiendo que las moléculas siguen la distribución de velocidades de Maxwell en vez de la velocidad media: \begin{equation} k=\frac{25\pi}{64}\lambda\bar{v}\rho\frac{C_{vm}}{N_A} \end{equation} Ecuación que resulta más manejable si hacemos las siguientes sustituciones: $\lambda=\frac{1}{\sqrt{2}\pi d^2}\frac{kT}{P}$; $\rho=\frac{N}{V}=\frac{P}{RT}$ y $\bar{v}=\left(\frac{8kT}{\pi m}\right)^{1/2}$: \begin{equation} k=\frac{25}{32}\left(\frac{RT}{\pi M}\right)^{1/2}\frac{1}{N_Ad^2}C_{vm} \end{equation}



