Oscilador armónico | Mecánica cuántica
- Detalles
- Escrito por: Germán Fernández
- Categoría: Oscilador armónico | Mecánica cuántica
- Visto: 1337
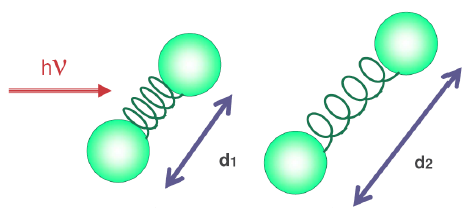El oscilador armónico es un sistema físico en el que una masa oscila en torno a una posición de equilibrio sometida a un potencial elástico \(V(x)=\frac{1}{2}kx^2\). La oscilación de los átomos de una molécula puede ser estudiada mediante la versión cuántica de este modelo. La resolución de la ecuación de Schrödinger nos proporciona los niveles de energía y la función de onda.
- Detalles
- Escrito por: Germán Fernández
- Categoría: Oscilador armónico | Mecánica cuántica
- Visto: 1325
Planteamos la ecuación de Schrödinger:
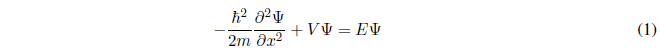
El oscilador armónico está sometido a un potencial del tipo: \(V(x)=\frac{1}{2}kx^2\)
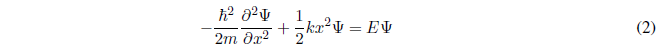
Despejando la derivada de mayor grado, la ecuación (2) puede escribirse:
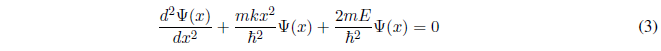
- Detalles
- Escrito por: Germán Fernández
- Categoría: Oscilador armónico | Mecánica cuántica
- Visto: 1177
La ecuación diferencial (16) tiene una solución del tipo:
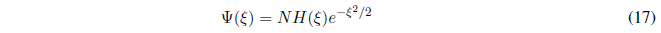
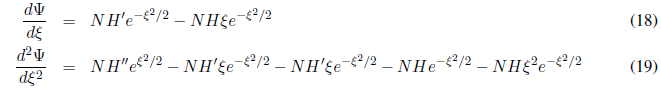
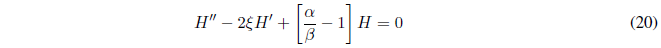
- Detalles
- Escrito por: Germán Fernández
- Categoría: Oscilador armónico | Mecánica cuántica
- Visto: 1427
Algunas expresiones que permiten calcular los polinomios de Hermite son: \begin{equation}\label{ec-34} H_v(\xi)=(2\xi)^v-v(v-1)(2\xi)^{v-2}+\frac{v(v-1)(v-2)(v-3)}{2}(2\xi)^{v-4}+...... \end{equation} La ecuación (\ref{ec-34}) puede escribirse de forma más compacta, como: \begin{equation}\label{ec-35} H_v(\xi)=\sum_{k=0}^{v}(-1)^k\frac{v!}{k!(v-2k)!}(2\xi)^{v-2k} \end{equation}
- Detalles
- Escrito por: Germán Fernández
- Categoría: Oscilador armónico | Mecánica cuántica
- Visto: 1224
Las funciones de onda del oscilador armónico vienen dadas por la ecuación (\ref{ec17}), donde N es la constante de normalización, que podemos calcular con la siguiente ecuación: \begin{equation}\label{ec-43} \int_{-\infty}^{+\infty}\Psi_{v}^{\ast}(x)\Psi_{v}(x)dx=1 \end{equation} La normalización de la función de onda para un estado general $v$ nos da el siguiente resultado: \begin{equation} N_v =\left(2^v v!\right)^{-1/2}\left(\frac{\beta}{\pi}\right)^{1/4} \end{equation}
- Detalles
- Escrito por: Germán Fernández
- Categoría: Oscilador armónico | Mecánica cuántica
- Visto: 1426
- Para el estado fundamental del oscilador armónico unidimensional, encontrar el valor promedio de las energías cinética y potencial. Comprobar que <T>=<V> en este caso. Hállense la posición más probable de la partícula para dicha función de onda y comprobar que se cumple el principio de incertidumbre. Datos:$\int_{0}^{\infty}x^2 e^{-\alpha x^2}dx=\pi^{1/2}/4\alpha^{3/2}$
- Haciendo uso de la fórmula de Rodrigues, genera los polinomios con $v=0,1,2,3....$
- El oscilador armónico tridimensional tiene la función de energía potencial $V(x,yz)=k_x \frac{x^2}{2} + k_y \frac{y^2}{2} + k_z \frac{z^2}{2}$, donde $k_x$, $k_y$ y $k_z$ son tres constantes de fuerza. Haciendo uso del método de separación de variables, encontrar las funciones propias y los valores propios de la energía de dicho oscilador.