Teoría Cuántica
- Detalles
- Escrito por: Germán Fernández
- Categoría: Teoría Cuántica
- Visto: 768
A finales del siglo XIX la física clásica era capaz de explicar casi todos los fenómenos físicos conocidos. Sin embargo, fenómenos como la radiación del cuerpo negro, el efecto fotoeléctrico, los espectros atómicos o el efecto Compton no tenían una explicación satisfactoria.
La razón por la que la física clásica es incapaz de explicar dichos fenómenos se debe a que no es una teoría adecuada para describir fenómenos a nivel atómico. En estas dimensiones se require de una nueva teoría, desarrollada durante el primer cuarto del siglo XX, llamada la teoría cuántica.
- Detalles
- Escrito por: Germán Fernández
- Categoría: Teoría Cuántica
- Visto: 1522
- Detalles
- Escrito por: Germán Fernández
- Categoría: Teoría Cuántica
- Visto: 995
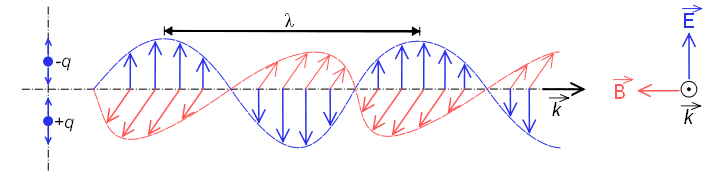
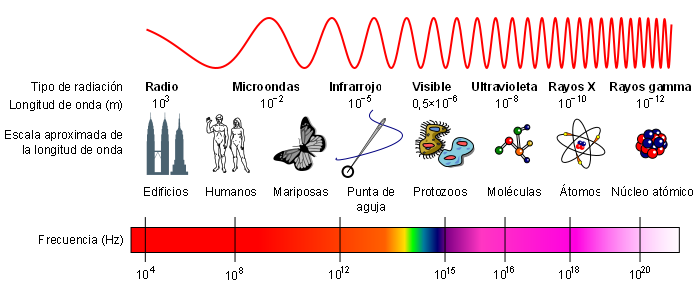
Se denomina espectro electromagnético a la distribución energética del conjunto de las ondas electromagnéticas.
El espectro electromagnético se extiende desde la radiación de menor longitud de onda, como los rayos gamma y los rayos X, pasando por la luz ultravioleta, la luz visible y los rayos infrarrojos, hasta las ondas electromagnéticas de mayor longitud de onda, como son las ondas de radio. Se cree que el límite para la longitud de onda más pequeña posible es la longitud de Planck mientras que el límite máximo sería el tamaño del Universo.
- Detalles
- Escrito por: Germán Fernández
- Categoría: Teoría Cuántica
- Visto: 871
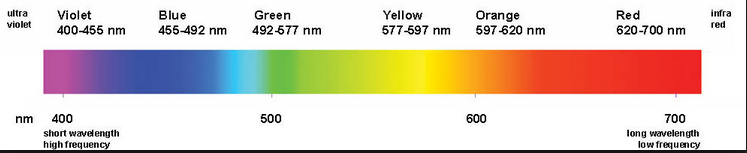
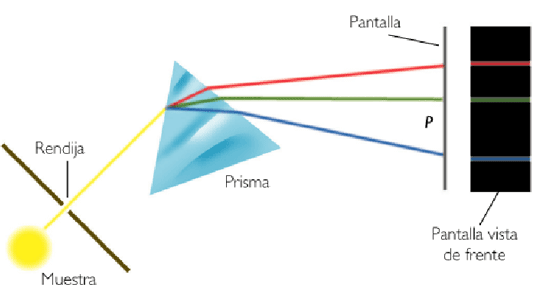
Cuando un haz de luz blanca pasa a través de un prisma las distintas longitudes de onda que la componen son refractadas de forma diferente, dispersando la luz en una banda de colores que corresponden a todas las longitudes de onda que la componen.
La radiación de mayor frecuencia (violeta) se refracta más que la radiación de menor frecuencia (rojo), dando lugar a la separación de la luz en las diferentes radiaciones que la componen, llamado espectro de la luz visible.
- Detalles
- Escrito por: Germán Fernández
- Categoría: Teoría Cuántica
- Visto: 2901
Cuando descomponemos la luz del sol mediante un prisma obtenemos un espectro continuo, formado por un elevado número de longitudes de onda.
Los gases, por el contrario, generan espectros discontinuos o de líneas. En la siguiente figura se muestra el espectro del helio, obtenido al excitar los átomos de helio mediante una descarga eléctrica, energía que absorben para emitirla posteriormente en forma de luz.
La luz emitida por los átomos de helio cuando se desexcitan pasas a través de una rendija, dispersándose en un prisma y siendo registrada mediante una película fotográfica.
Cada elemento químico tiene un espectro característico, que permite identificarlo. Así, el helio (del griego, helios, significa sol) fue descubierto durante un eclipse solar, 27 años antes de ser aislado.
- Detalles
- Escrito por: Germán Fernández
- Categoría: Teoría Cuántica
- Visto: 7017
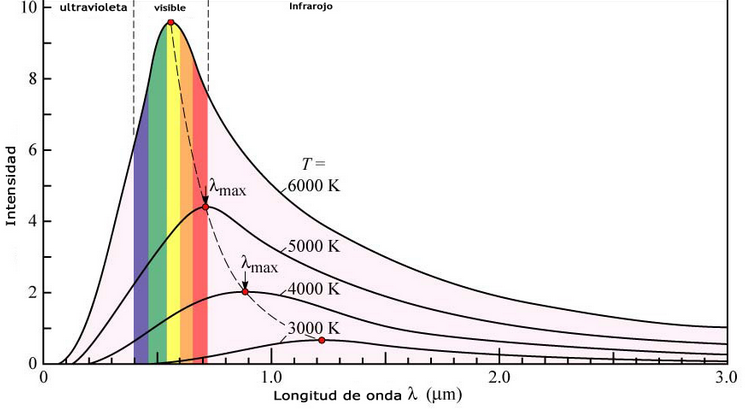
Otro fenómeno que la física clásica no podía explicar era la emisión de radiación por parte de un cuerpo negro. Un cuerpo negro es un objeto capaz de absorber toda la radiación que le llega sin reflejar nada. La intensidad de la radiación emitida por un cuerpo negro varía con la longitud de onda según una curva característica que presenta un máximo dependiente de la temperatura del cuerpo. Según la teoría clásica la intensidad de la radiación emitida por el cuerpo negro debe aumentar, según disminuye la longitud de onda, haciéndose infinita, comportamiento que carece de sentido físco.
- Detalles
- Escrito por: Germán Fernández
- Categoría: Teoría Cuántica
- Visto: 2164
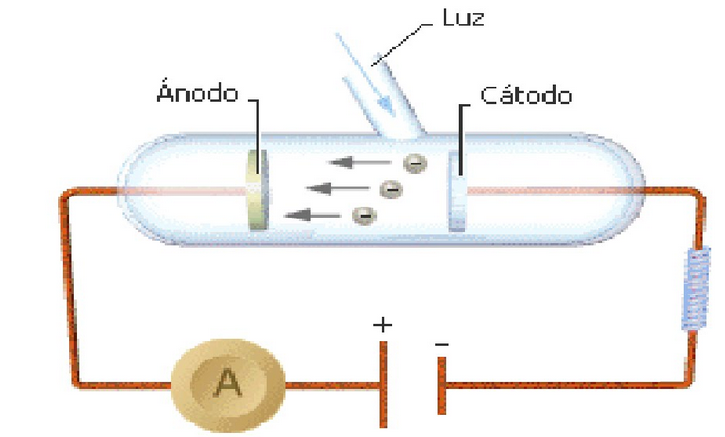
Es un fenómeno físico que consiste en la emisión de electrones por ciertos metales cuando un haz de luz incide sobre su superficie. Fue observado en 1888 por Heinrich Hertz.
El efecto fotoeléctrico se caracteriza por:
- Para que la emisión de electrones se produzca es necesario que la luz incidente tenga una frecuencia mínima, llamada frecuencia umbral $\nu_0$
- El número de electrones emitido dependende de la intensidad de la radiación incidente.
- La energía cinética de los electrones depende de la frecuencia de la luz.
- Detalles
- Escrito por: Germán Fernández
- Categoría: Teoría Cuántica
- Visto: 3200
En 1924, el francés Victor de Broglie publicó su tesis doctoral, en la que desarrollaba la hipótesis de que las partículas de materia podían presentar un comportamiento ondulatorio. De Broglie se inspiró en el trabajo de Einstein sobre el efecto fotoeléctrico, en el que la luz estaba formada por pequeños corpúsculos llamados fotones, cuya energía era $h\nu$. Si un fenómeno claramente ondulatorio como la luz tenía ese comportamiento corpuscular, quizá fuera posible que las partículas de materia tengan un comportamiento ondulatorio.
Igualando la ecuación de Einstein, $E=mc^2$ a la de Planck, $E=h\nu$:
$mc^2=h\nu$, reemplazando la frecuencia por $\nu=c/\lambda$:
$mc^2=h\frac{c}{\lambda}$, despejando la longitud de onda:
\begin{equation}\lambda=\frac{h}{mc}=\frac{h}{p}\end{equation}
Siendo p la cantidad de movimiento o momento lineal de la partícula.
Esta ecuación nos indica que toda partícula que posea cantidad de movimiento, fotón, electrón, protón, posee una onda asociada de longitud $\lambda$.
Lee más: Dualidad onda-corpúsculo | Hipótesis de Louis de Broglie
- Detalles
- Escrito por: Germán Fernández
- Categoría: Teoría Cuántica
- Visto: 1587
El modelo atómico de Rutherford, estudiado en una sección anterior, no explica cómo se distribuyen los electrones en el átomo. Además, según la física clásica una partícula cargada y en movimiento -los electrones- emite radiación electromagnética, perdiendo su energía y terminando por caer sobre el núcleo.
El modelo atómico de Bohr resuelve estos problemas basándose en la hipótesis de Planck de la cuantización de la energía.
El modelo de Bohr se fundamenta en los siguientes postulados:
- El electrón se mueve en torno al núcleo en órbitas circulares.
- Las orbitas permitidas para el electrón, en las que no emite energía, son aquellas en las que el momento angular toma valores $n\hbar$, donde n es un número entero. La primera órbita del electrón tiene n=1, la segunda n=2, etc.
- El electrón pasa de unas orbitas a otras mediante la absorción o emisión de cuantos de energía.
- Detalles
- Escrito por: Germán Fernández
- Categoría: Teoría Cuántica
- Visto: 1699
En el mundo clásico podemos medir con precisión la cantidad de movimiento y la posición de una partícula. Sin embargo, en el mundo cuántico
estas magnitudes se ven afectadas por una incertidumbre que impide conocer simultáneamente sus valores. El conocimiento de la posición de la partícula produce un desconocimiento en su cantidad de movimiento o velocidad. Llamando $\Delta x$ a la incertidumbre en la posición y $\Delta p$ a la incertidumbre en su cantidad de movimiento, podemos escribir la expresión del principio de incertidumbre como sigue:
\begin{equation} \Delta x \cdot \Delta p\geq \frac{h}{4\pi} \end{equation}
- Detalles
- Escrito por: Germán Fernández
- Categoría: Teoría Cuántica
- Visto: 1433
En 1927, Erwin Schrödinger propuso que cualquier electrón o partícula que posea propiedades ondulatorias puede ser descrito mediante una función, representada por la letra griega psi, $\psi$, llamada función de onda o estado y contiene toda la información que es posible conocer sobre ese sistema cuántico.
La ecuación de Schrödinger, $\hat{H}\psi=E\psi$, es una ecuación diferencial cuya solución nos da la función de onda del sistema y su energía. En esta ecuación, $\hat{H}$, representa al operador hamiltoniano, cuya expresión para un sistema unidimensional es:
\begin{equation} \hat{H}=-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}+V \end{equation}
siendo, $\hbar=h/2\pi$ y V el potencial al que está sometida la partícula.
El significado físico de la función de onda lo da su módulo al cuadrado, llamado densidad de probabilidad, $|\psi|^2$, y relacionado con la probabilidad de encontrar la partícula en una determinada zona del espacio.
Vídeo:
- Detalles
- Escrito por: Germán Fernández
- Categoría: Teoría Cuántica
- Visto: 1249
Se trata de una partícula confinada en el intervalo [0,a] sobre el eje x. Dentro de este intervalo el potencial al que está sometida es cero, mientras que fuera del intervalo es infinito.
La resolución de la ecuación de Schrödinger para este modelo nos da la función de onda y la energía.
\begin{equation} \psi_n=\sqrt\frac{2}{a}sen\frac{n\pi x}{a} \end{equation}
\begin{equation} E_n=\frac{h^2n^2}{8ma^2} \end{equation}
siendo n=1,2,3...., el número que cuantiza la energía.
- Detalles
- Escrito por: Germán Fernández
- Categoría: Teoría Cuántica
- Visto: 1879
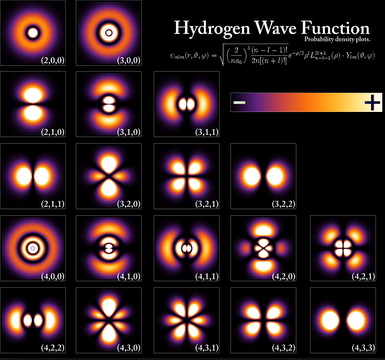
La solución de la ecuación de Schrödinger para el átomo de hidrógeno nos proporciona unas funciones de onda, llamadas orbitales, y unos niveles de energía permitidos. Dada la simetría del problema es aconsejable el uso de coordenadas esféricas ($r,\theta,\varphi$). El conjunto de funciones de onda hidrogenoides tienen la siguiente forma: \begin{equation} \psi_{nlm}(r,\theta,\varphi)=R_{nl}(r)Y_{lm}(\theta,\varphi) \end{equation}
La función $R_{nl}(r)$ se denomina función de onda radial y la función $Y_{lm}(\theta,\varphi)$ se conoce como función de onda angular y pertenece a la familia de los armónicos esféricos. n, l y m son los números cuánticos que surgen al resolver la ecuación de Schrödinger y determinan el tipo de orbital.
- n: número cuántico principal, toma valores enteros, positivos y distintos de cero. Representa los niveles de energía en el átomo hidrogenoide. n=1,2,3...
- l: número cuántico del momento angular orbital, toma valores comprendidos entre 0 y n-1. l=0,1,2....
- m: número cuántico magnético, está asociado a la componente z del momento angular y toma valores entre -l y +l. m=-l, -l+1,....0......l-1, l
- Detalles
- Escrito por: Germán Fernández
- Categoría: Teoría Cuántica
- Visto: 1761
Según la interpretación de Born el módulo al cuadrado de la función de onda nos da la densidad de probabilidad, probabilidad de encontrar la partícula en unas determinadas coordenadas. En esta sección vamos a representar las densidades de probabilidad de los orbitales mediante superficies que contienen la mayor parte de la probabilidad de encontrar el electrón.
Recordemos que las funciones de onda hidrogenoides se componen del producto de una parte radial $R(r)$ por una parte angular $Y(\theta,\varphi)$, denominada armónico esférico. La parte radial depende de los números cuánticos n y l, mientras que la parte angular la hace de l y m.
Para obtener la función de onda del estado fundamental del átomo de hidrógeno multiplicamos la función radial $R(1s)=2(Z/a)^{3/2}e^{-Zr/a}$ por el armónico esférico $Y_{00}=1/\sqrt{4\pi}$:
\begin{equation} \psi_{1s}=\frac{1}{\sqrt{\pi}}\left(\frac{Z}{a}\right)^{3/2}e^{-Zr/a} \end{equation}
En el caso del átomo de hidrógeno Z=1, y la ecuación para la función de onda nos queda:
\begin{equation} \psi_{1s}=\frac{1}{\sqrt{\pi}}\left(\frac{1}{a_0}\right)^{3/2}e^{-r/a_0} \end{equation}
Elevando al cuadrado la función de onda obtenemos la densidad de probabilidad:
\begin{equation} \psi^2(1s)=\frac{1}{\pi a_0^3}e^{-2r/a_0} \end{equation}
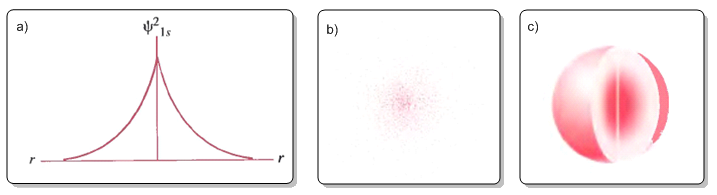
En la figura (a) se representa la densidad de probabilidad electrónica $\psi^2$ frente a r. La figura (b) representa la densidad de probabilidad como densidad de puntos. La figura (c) es la tipica representación del orbital 1s en la que se delimita la zona del espacio con una probabilidad de encontrar el electrón de 0,9.
- Detalles
- Escrito por: Germán Fernández
- Categoría: Teoría Cuántica
- Visto: 1254
El espín es una propiedad intrínseca del electrón que inicialmente se asoció a una rotación, pero dado que no depende de coordendas espaciales es independiente del estado de movimiento de la partícula. El valor del momento angular de espín está cuantizado, dependiendo de un número cuántico, $m_s$ que toma valores +1/2 y -1/2.
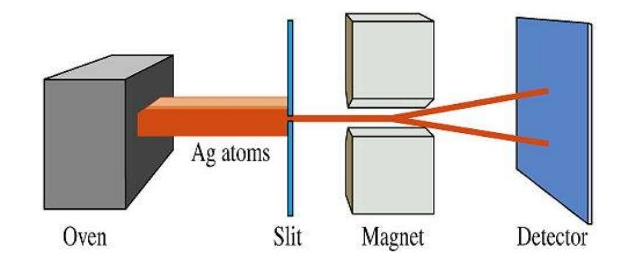
La demostración experimental de la existencia del espín la realizarón Stern y Gerlach en 1920. Al someter un haz de átomos de plata, vaporizados en un horno, a un campo magnético variable, observaron el desdoblamiento del haz en dos haces, debido a la presencia de un electrón desapareado que en la mitad de los átomos de plata tiene $m_s=1/2$ y en la otra mitad $m_s=-1/2$.
Vídeo:
- Detalles
- Escrito por: Germán Fernández
- Categoría: Teoría Cuántica
- Visto: 1986
Como vimos en secciones anteriores los niveles de energía del átomo de hidrógeno vienen dados por el número cuántico principal (n), siendo independientes de los números cuánticos l y m. Esta situación cambia en átomos con más de un electrón debido a la interacción entre ellos. En átomos polielectrónicos la energía del electrón depende también del número cuántico l, estándo situados en diferente nivel de energía los electrones de la subcapa 2s y los de la 2p. De igual modo presentan diferente energía los 3s, 3p y 3d.
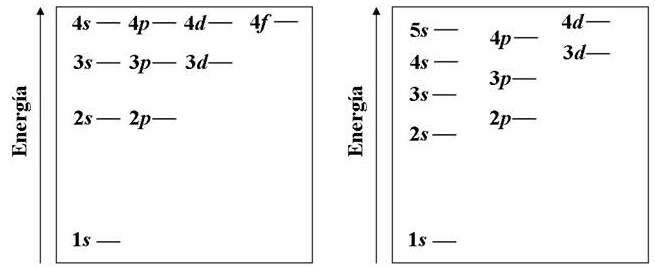
En el diagrama de la izquierda se representan los niveles de energía de los átomos hidrogenoides (un sólo electrón). A la derecha tenemos los niveles de energía para un átomo polielectrónico.
Vídeo:
- Detalles
- Escrito por: Germán Fernández
- Categoría: Teoría Cuántica
- Visto: 6458
La configuración electrónica de un átomo nos indica como se distribuyen los electrones en las diferentes capas, subcapas y orbitales. Esta distribución está relacionada con las propiedades físicas de los elementos. Para escribir la configuración electrónica de un átomo polielectrónico utilizaremos tres reglas: 1/ Regla de llenado o aufbau; 2/ Principio de exclusión de Pauli; 3/ Regla de Hund de la máxima multiplicidad.
- Regla de llenado o aufbau. Los electrones ocupan los orbitales de manera que se minimice la energía del átomo. Es decir, primero se ocupan los niveles de menor energía. El orden de llenado de las diferentes subcapas se obtiene mediante el siguiente diagrama en el que debemos comenzar por la linea superior e ir siguiendo las flechas.
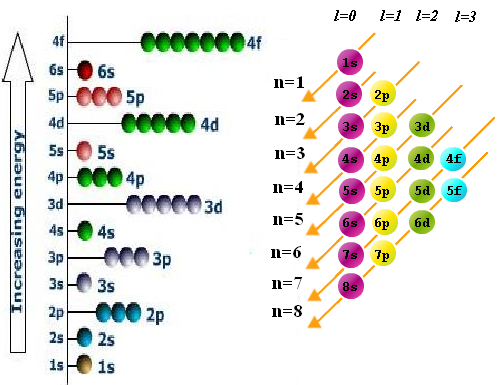
Lee más: Configuración electrónica de los átomos polielectrónicos
- Detalles
- Escrito por: Germán Fernández
- Categoría: Teoría Cuántica
- Visto: 4866
Los electrones internos del átomo "bloquean la vista" (apantallan) del núcleo a electrones más externos, sintiendo una carga nuclear inferior a la que realmente tiene el núcleo, llamada carga nuclear efectiva $(Z_ef)$. Para calcular la carga nuclear efectiva restamos la carga real del núcleo (número atómico, Z) del apantallamiento que producen los electrones internos (S). \begin{equation} Z_{ef}=Z-S \end{equation} Los electrones que se encuentran en orbitales más intenos (penetran más en el átomo), con mayor densidad electrónica en las proximidades del núcleo apantallan más a los electrones externos que electrones que se encuentran en orbitales con una densidad electrónica más alejada del núcleo. Por ejemplo, el orbital 1s es el de mayor penetración del átomo, sus electrones están muy cercanos al núcleo y producen un importante efecto pantalla sobre electrones externos. Los siguientes en orden de penetración son los 2s, le siguen los 2p....
Orden de penetración de orbitales: 1s>2s>2p>3s>3p>3d.
Lee más: Carga nuclear efectiva, apantallamiento y reglas de Slater
- Detalles
- Escrito por: Germán Fernández
- Categoría: Teoría Cuántica
- Visto: 1077