Teoría cinética de los gases
- Detalles
- Escrito por: Germán Fernández
- Categoría: Teoría cinética de los gases
- Visto: 4918
La teoría cinética de los gases permite deducir las propiedades del gas ideal empleando un modelo en el que las moléculas del gas son esferas que cumplen las leyes de la mecánica clásica.
Las propiedades calculables mediante este modelo son: presión del gas, distribución de velocidades moleculares, velocidad molecular media, velocidad de colisión y distancia media entre colisiones. Estas propiedades permiten el estudio de la cinética de reacciones en fase gaseosa así como el flujo de fluidos y la transmisión de calor.
Fundamentos de la teoría cinético-molecular de los gases
La teoría cinética puede considerarse como una rama de la termodinámica estadística ya que deduce propiedades macroscópicas de la materia a partir de propiedades moleculares. Los principios en los que se fundamenta son los siguientes:
- Un gas está formado por un gran número de partículas esféricas cuyo tamaño es despreciable comparado con la distancia entre las partículas.
- Las moléculas se mueven en línea recta a gran velocidad y sólo interaccionan cuando colisionan. Los choques entre partículas y con las paredes del recipiente se consideran perfectamente elásticos, conservándose la energía cinética traslacional.
- La teoría cinética supone que las partículas obedecen las leyes de Newton. Esta suposición es incorrecta (las moléculas cumplen las leyes de la mecánica cuántica) y conduce a resultados incorrectos en la predicción de las capacidades caloríficas del gas, aunque da resultados aceptables en propiedades como presión o difusión.
- Detalles
- Escrito por: Germán Fernández
- Categoría: Teoría cinética de los gases
- Visto: 2170
Las funciones de distribución de velocidades nos van a permitir conocer la fracción de moléculas con velocidades comprendidas entre dos valores dados.
Vamos a utilizar 3 funciones de distribución :
- Para los componentes de la velocidad $g(v_x),g(v_y)$ y $g(v_z)$.
- Para el vector velocidad $\phi(\vec{v})$
- Para el módulo de la velocidad $G(v)$.
Funciones de distribución de las componentes de la velocidad $g(v_x),g(v_y)$ y $g(v_z)$
La función de distribución $g(v_x)$ permite conocer la fracción de moléculas con velocidades comprendidas entre $v_x$ y $v_x+dv_x$.
\begin{equation} dN_{v_{x}}/N=g(v_x)dv_x \end{equation}
Pueden escribirse ecuaciones análogas para las funciones de distribución en dirección y,z
\begin{equation} dN_{v_{y}}/N=g(v_y)dv_y \end{equation}
\begin{equation} dN_{v_{z}}/N=g(v_z)dv_z \end{equation}
- Detalles
- Escrito por: Germán Fernández
- Categoría: Teoría cinética de los gases
- Visto: 2138
La probabilidad de encontrar una molécula en un determinado nivel energético, j, viene dada por:
\begin{equation} p_j=\frac{e^{-\epsilon_j/kT}}{\sum e^{-\epsilon_i/kT}} \end{equation}
Desde el punto de vista clásico la energía cinética de una molécula varía de forma continua y viene dada por la expresión $\epsilon_x=\frac{1}{2}mv_x^2$. Llevando este valor de energía a la expresión de la probabilidad se obtiene:
\begin{equation} dp(v_x)=\frac{dN_{v_x}}{N}=\frac{e^{-\frac{mv_x^2}{2kT}}dv_x}{\int_{-\infty}^{\infty}e^{-\frac{mv_x^2}{2kT}}dv_x} \end{equation}
Donde, $dp(v_x)$ representa la fracción de moléculas con velocidad comprendida entre $v_x$ y $v_x+dv_x$. La integral del denominador representa la suma a lo largo de todos los posibles valores de $v_x$ y tiene la forma $\int e^{-bx}dx=(\pi/b)^{1/2}$
\begin{equation} dp(v_x)=\frac{dN_{v_x}}{N}=\frac{e^{-\frac{mv_x^2}{2kT}}dv_x}{\left(\frac{2\pi kT}{m}\right)^{1/2}} \end{equation}
Lee más: Obtención de la función de distribución para $v_x$, $g(v_x)$
- Detalles
- Escrito por: Germán Fernández
- Categoría: Teoría cinética de los gases
- Visto: 1643
La probabilidad de que una molécula tenga su componente de velocidad en dirección x comprendida entre $v_x$ y $v_{x+dx}$, en dirección y entre $v_y$ y $v_{y+dy}$ y en dirección z entre $v_z$ y $v_{z+dz}$ vendrá dada por: \begin{equation} dN_{v_x,v_y,v_z}/N=g(v_x)g(v_y)g(v_z)dv_xdv_ydv_z \end{equation} $dN_{v_x,v_y,v_z}/N$ representa la probabilidad de que una molécula (fracción de moléculas) tenga el extremo de su vector velocidad en el interior de una caja de lados $dv_x, dv_y, dv_z$
Sustituyendo las expresiones calculadas anteriormente para las funciones de distribución en cada dirección espacial: \begin{equation} \phi(\bar{v})=g(v_x)g(v_y)g(v_z)=\left(\frac{m}{2\pi kT}\right)^{1/2}e^{-mv^2/2kT} \end{equation} Siendo, $v^2=v_x^2+v_y^2+v_z^2$, el cuadrado del módulo de la velocidad. Esta nueva función de distribución no depende de la orientación del vector, sino exclusivamente de su módulo.
- Detalles
- Escrito por: Germán Fernández
- Categoría: Teoría cinética de los gases
- Visto: 1855
En esta sección vamos a deducir la ecuación que nos permite conocer la fracción de moléculas que tienen el módulo de su velocidad comprendida entre dos valores determinados.
Llamamos $dN_v/N$ a la fracción de moléculas con velocidad comprendida entre v y v+dv. Donde N representa el número total de moléculas del gas. \begin{equation} \frac{N_v}{N}=G(v)dv \end{equation} G(v) es la función de distribución de velocidades o densidad de probabilidad. Al multiplicar esta función por $dv$ se obtiene la fracción de moléculas con velocidad comprendida entre v y v+dv.
Si nos interesa calcular la fracción de moléculas con velocidad comprendida entre $v_1$ y $v_2$, integramos la función de distribución de velocidades en ese intervalo. (Es equivalente hablar de fracción de moléculas que tienen su velocidad en un intervalo dado y probabilidad de que una molécula tenga su velocidad comprendida en dicho intervalo) \begin{equation} P[v_1,v_2]=\int_{v_1}^{v_2}G(v)dv \end{equation} La probabilidad de que una molécula tenga su velocidad comprendida en el intervalo $[0,\infty]$ es 1 \begin{equation} \int_{0}^{\infty}G(v)dv=1 \end{equation}
Lee más: Obtención de la función de distribución del módulo de la velocidad $G(v)$
- Detalles
- Escrito por: Germán Fernández
- Categoría: Teoría cinética de los gases
- Visto: 1568
\begin{equation} \bar{v}=\int_{0}^{\infty}vG(v)dv=4\pi\left(\frac{m}{2\pi kT}\right)^{3/2}\int_{0}^{\infty}e^{-mv^2/2kT}v^3dv \end{equation} Utilizando la integral $\int_{0}^{\infty}x^{2n+1}e^{-ax^2}dx=\frac{n!}{2a^{n+1}}$ \begin{equation} \bar{v}=4\pi\left(\frac{m}{2\pi kT}\right)^{3/2}\frac{1}{2(m/2kT)^2}=\left(\frac{8kT}{\pi m}\right)^{1/2} \end{equation} Multiplicando y dividiendo por el número de avogadro y teniendo en cuenta que $kN_A=R$ y $N_A m=M$ \begin{equation} \bar{v}=\left(\frac{8RT}{\pi M}\right)^{1/2} \end{equation}
- Detalles
- Escrito por: Germán Fernández
- Categoría: Teoría cinética de los gases
- Visto: 1827
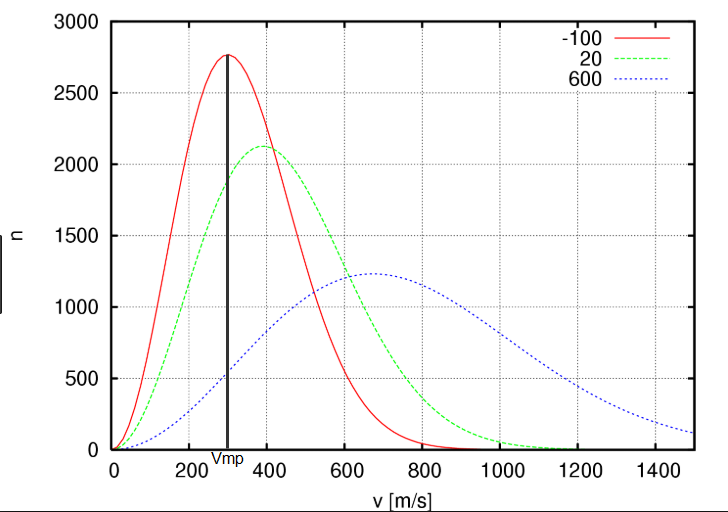
La velocidad más probable es la velocidad a la que es máxima la función G(v) y se obtiene igualando a cero la derivada de G(v) respecto de v. \begin{equation} \frac{dG(v)}{dv}=0\;\;\rightarrow \;\;v_{mp}=\left(\frac{2RT}{M}\right)^{1/2} \end{equation}
- Detalles
- Escrito por: Germán Fernández
- Categoría: Teoría cinética de los gases
- Visto: 1952
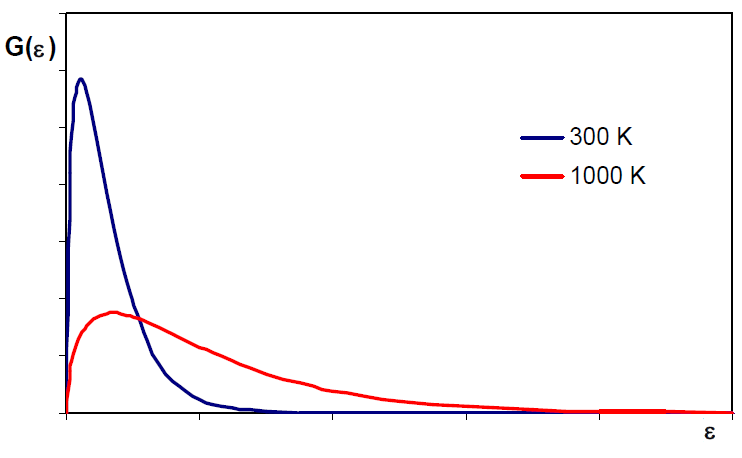
La distribución de Maxwell puede escribirse en función de energías traslacionales $\epsilon_{tr}=\frac{1}{2}mv^2$, despejando v, $v=\left(\frac{2\epsilon_{tr}}{m}\right)^{1/2}$, derivando: \begin{equation} dv=\left(\frac{2}{m}\right)^{1/2}\frac{1}{2}\epsilon_{tr}^{-1/2}d\epsilon_{tr}=\left(\frac{1}{2m}\right)^{1/2}\frac{d\epsilon_{tr}}{\epsilon_{tr}^{1/2}} \end{equation} Sustituyendo v y dv en $\frac{dN_v}{N}=\left(\frac{m}{2\pi mkT}\right)^{3/2}e{\frac{-mv^2}{2kT}}4\pi v^2dv$ \begin{equation} \frac{dN_{\epsilon_{tr}}}{N}=\left(\frac{m}{2\pi mkT}\right)^{3/2}e^{\frac{-m(2\epsilon_{tr}/m)}{2kT}}4\pi \left(\frac{2\epsilon_{tr}}{m}\right)\left(\frac{1}{2m}\right)^{1/2}\frac{d\epsilon_{tr}}{\epsilon_{tr}^{1/2}} \end{equation} Simplificando: \begin{equation} \frac{dN_{\epsilon_{tr}}}{N}=2\pi \left(\frac{1}{\pi kT}\right)^{3/2}e^{\frac{-\epsilon_{tr}}{kT}\epsilon_{tr}^{1/2}}d\epsilon_{tr} \end{equation} $dN_{\epsilon_{tr}}$ representa el número de moléculas cuya energía traslacional está comprendida entre $\epsilon_{tr}$ y $\epsilon_{tr}+d\epsilon_{tr}$
La energía traslacional media es la misma para todos los gases a la misma temperatura.
- Detalles
- Escrito por: Germán Fernández
- Categoría: Teoría cinética de los gases
- Visto: 2202
Vamos a calcular la frecuencia de colisión de las moléculas de un gas con la pared de un recipiente en un dt.
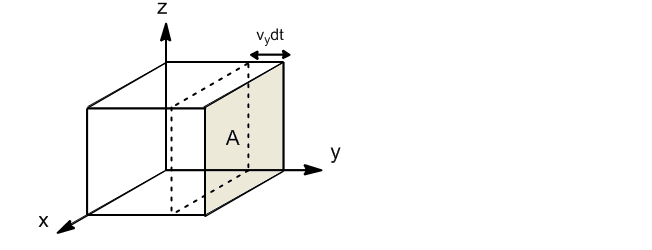
Si tomamos la pared perpendicular al eje y, sólo las moléculas con componente y de velocidad chocarán contra dicha pared. La fracción de moléculas con componente y de velocidad comprendida entre $v_y$ y $v_y+dv_y$ viene dada por: \begin{equation} \frac{dN_{v_y}}{N}=g(v_y)dv_y \end{equation} Solamente las moléculas que se encuentran a una distancia $v_ydt$ de la pared podrán chocar contra ella en el dt. El volumen de la caja en el que se encuentran las moléculas que pueden chocar contra la pared sera: $V'=Av_ydt$. Dividiendo este voluen entre el total $V'/V$ se obtiene la fracción de moléculas que por su proximidad a la pared pueden chocar.
- Detalles
- Escrito por: Germán Fernández
- Categoría: Teoría cinética de los gases
- Visto: 3458
Si un recipiente que contiene un gas tiene un pequeño agujero de área $A_{or}$ y en el exterior del recipiente hay vacío, las moléculas que chocan con el agujero escapan del recipiente a una velocidad que viene dada por: \begin{equation} \frac{dN}{dt}=\frac{-A_{or}P}{\left(2\pi mkT\right)^{1/2}} \end{equation} El signo menos indica que las moléculas salen del recipiente. A este fenómeno se le denomina efusión, siendo las velocidades de efusión inversamente proporcionales a las raices cuadradas de las masas moleculares.
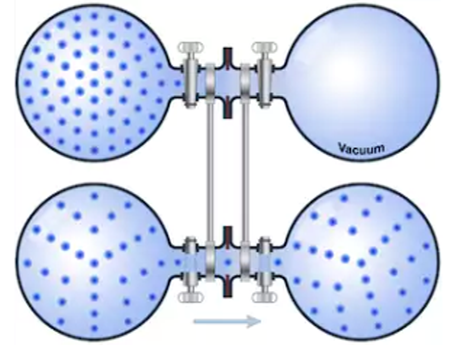
Para que se cumpla la Ley de Graham es necesario que el orificio sea muy pequeño, para que el gas se escape lentamente y no rompa la ditribución Maxweliana de velocidades. El diámetro del agujero debe ser sustancialmente menor que la distancia que las moléculas del gas recorren entre dos colisiones (recorrido medio libre), para evitar que choquen unas con otras en las proximidades del orificio, lo que daría lugar a un flujo colectivo que rompe la distribución de Maxwell
- Detalles
- Escrito por: Germán Fernández
- Categoría: Teoría cinética de los gases
- Visto: 2556
Se mide la presión de vapor de un líquido determinando la velocidad de efusión del gas en equilibrio con él. Para ello se mide la pérdida de peso w en el interior debido a las moléculas que escapan. \begin{equation} \frac{dw}{dt}=m\frac{dN}{dt}=-\frac{A_{or}P_vm}{(2\pi mkT)}^{1/2}=-P_vA_{or}\left(\frac{m}{2\pi kT}\right)^{1/2} \end{equation} En un intervalo de tiempo finito $\Delta t$, se producirá la siguiente pérdida de peso: \begin{equation} \Delta w=-P_vA_{or}\left(\frac{m}{2\pi kT}\right)^{1/2}\Delta t \end{equation} Pesando el recipiente al principio y al final del experimento determinamos $\Delta w$ y utilizando la ecuación anterior la presión de vapor. \begin{equation} P_v=\frac{\Delta w}{A_{or}\Delta t}\left(\frac{2\pi kT}{m}\right)^{1/2} \end{equation}
- Detalles
- Escrito por: Germán Fernández
- Categoría: Teoría cinética de los gases
- Visto: 5342
La teoría cinética permite calcular la frecuencia de colisiones entre moléculas. Suponemos que las moléculas son esferas rígidas de diámetro d y despreciamos las fuerzas intermoleculares excepto en el momento de la colisión. A presiones elevadas las fuerzas intermoleculares no pueden ser despreciadas y las ecuaciones obtenidas no son aplicables. Utilizaremos la siguiente notación:
- $z_{12}$: número de colisiones por unidad de tiempo (frecuencia de colisiones) que una molécula del gas 1 experimenta con las moléculas del gas 2.
- $z_{11}$: frecuencia de colisiones que una molécula del gas 1 experimenta con otras moléculas del gas 1.
- $Z_{12}$: frecuencia total de colisiones entre moléculas del gas 1 con las del gas 2 por unidad de volumen.
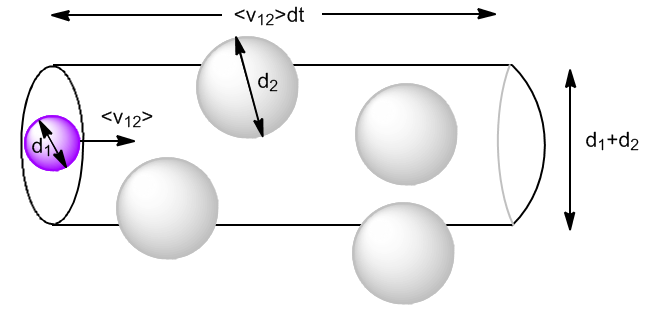
Sean $N_1$ moléculas del gas 1 con diámetro $d_1$ y $N_2$ moléculas del gas 2 con diámetro $d_2$. Las moléculas se mueven a velocidades medias $\bar{v}_1$ y $\bar{v}_2$.
Comenzamos calculando las colisiones de las moléculas tipo 1 con las tipo 2 $(z_{12})$. Consideremos las moléculas de tipo 2 en reposo y las de tipo 1 moviéndose a velocidad $\bar{v}_{12}$, velocidad media relativa de las moléculas tipo 1 respecto a las tipo 2.
- Detalles
- Escrito por: Germán Fernández
- Categoría: Teoría cinética de los gases
- Visto: 2058
Se define como la distancia que una molécula avanza entre dos colisiones sucesivas. Sea $\bar{v}_1$ la velocidad media de las moléculas tipo 1. En un tiempo t recorre una distancia $\bar{v}_1t$ siendo el número de colisiones $[z_{11}+z_{12}]t$. Por tanto, la distancia media recorrida por una molécula 1 entre dos colisiones es: \begin{equation} \lambda=\frac{\bar{v}_1}{z_{11}+z_{12}} \end{equation} Si el gas es puro: \begin{equation} \lambda=\frac{\bar{v}_1}{z_{11}}=\frac{1}{\sqrt{2}\pi d_1^2}\frac{V}{N_1} \end{equation} Utilizando la ecuación PV=NkT, V/N=kT/P. \begin{equation} \lambda=\frac{1}{\sqrt{2}\pi d_1^2}\frac{kT}{P} \end{equation}