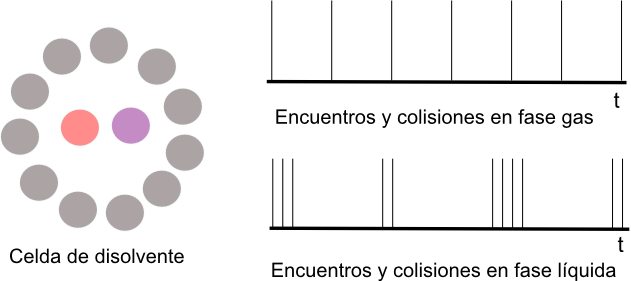Cinética química
- Detalles
- Escrito por: Jordi
- Categoría: Cinética química
- Visto: 3796
La cinética de las reacciones químicas es la parte de la química que se encarga del estudio de la rapidez con la que tienen lugar las reacciones (i), uno de los temas más importantes en cualquier proceso químico. El conocimiento de las velocidades de reacción es importante no sólo por sí mismo, sino también para la industria química, para comprender procesos bioquímicos importantes para la vida y en otros campos de aplicación. Por lo tanto, debemos definir qué es eso de la rapidez con que transcurre una reacción y aprender a medirla, así como descubrir qué relaciones existen entre la rapidez de las reacciones y el equilibrio químico. Pero sobre todo, debemos saber cómo tienen lugar las reacciones y cuáles son los procesos microscópicos que corresponden a los cambios en las especies químicas. Dado que la mayoría de las reacciones se producen a través de colisiones moleculares de algún tipo, es importante también estudiar la naturaleza de estas colisiones y la cinética química participa en dicho estudio.
i R.S.Berry, S.A.Rice y J.Ross - “Physical Chemistry - Part 3 – Physical and Chemical Kinetics”, 1ª ed, 1980 – J.Wiley & Sons – (pág. 1117).
- Detalles
- Escrito por: Jordi
- Categoría: Cinética química
- Visto: 6200
Consideremos una reacción química del tipo genérico:
$$a\ A + b\ B \rightleftharpoons c\ C + d\ D$$
donde $a$, $b$, $c$ y $d$ son los coeficientes estequiométricos. Intuitivamente podríamos entender que ha de existir un concepto tal como la velocidad de reacción que sea capaz de medir la rapidez con que tiene lugar una reacción determinada. Pero, formalmente, ¿cómo podríamos definir la velocidad de reacción? Por ejemplo, si nos fijamos en el reactivo $A$, podemos decir que la velocidad de reacción es la velocidad con que disminuye su concentración total en el medio. Es decir, que la velocidad de reacción sería la velocidad a la que desaparece el reactivo $A$, que viene dada por:
$$v_A = -\ \frac{d[A]}{dt}$$
Pero esta forma de definición presenta un problema. Consideremos ahora el producto de reacción $C$. Podríamos definir del mismo modo la velocidad de reacción como la velocidad con que aumenta la concentración total de $C$ en el medio, es decir, como la cantidad:
$$v_C = \frac{d[C]}{dt}$$
¿Y cuál es el problema? Pues que por cada $a$ moles del reactivo $A$ que desaparecen en un determinado período de tiempo, del producto $C$ habrán aparecido $c$ moles. Es decir que:
$$-\ \frac{1}{a}\ \cdot\ \frac{d[A]}{dt} = \frac{1}{c}\ \cdot\ \frac{d[C]}{dt}$$
- Detalles
- Escrito por: Jordi
- Categoría: Cinética química
- Visto: 3205
Consideremos el caso de una reacción química genérica:
$$a\ A + b\ B\ \rightleftharpoons\ c\ C + d\ D$$
De todas las variables que afectan a la velocidad de reacción, normalmente se suele hacer más hincapié en las concentraciones de las sustancias que toman parte en la reacción. Si se mantienen constantes variables como la temperatura, la presión y otras, entonces se puede determinar experimentalmente que la velocidad de una reacción es una función simple de dichas concentraciones. Experimentalmente, se puede comprobar que, en la mayoría de los casos, la velocidad es directamente proporcional al producto de determinadas potencias enteras de las concentraciones:
$$v = k\ \cdot\ [A]^{\alpha}\ \cdot\ [B]^{\beta}\ \cdot\ [C]^{\gamma}\ \cdot\ ...$$
Lee más: Ecuación de la Velocidad de Reacción (Ecuación cinética)
- Detalles
- Escrito por: Jordi
- Categoría: Cinética química
- Visto: 11163
Un concepto muy útil en el estudio de la cinética de una reacción es el tiempo de vida media. Este concepto se utiliza en muchos otros campos. El más conocido quizás sea el estudio de los procesos de desintegración radiactiva. Dichos procesos son, desde nuestro punto de vista, reacciones de primer orden, ya que la velocidad de desintegración de un radionúclido sólo depende de la cantidad de éste presente en la muestra.
Definiremos el tiempo de vida media de un reactivo como el tiempo necesario para que haya reaccionado la mitad de su concentración inicial. Suele representarse como $t_{1/2}$.
En el caso de una reacción de primer orden, cuya ecuación de velocidad sabemos que es:
$$v = k \cdot [A]$$
Entonces, según la definición de $t_{1/2}$, tenemos que:
$$t = t_{1/2} \Longrightarrow [A] = \frac{[A]_0}{2}$$
Usando la fórmula logarítmica para las reacciones de primer orden:
$$\ln [A] = \ln [A]_0 - k \cdot t$$
tendremos que:
$$\ln \frac{[A]_0}{2} = \ln [A]_0 - k \cdot t_{1/2}$$
por lo que:
$$\ln [A]_0 - \ln 2 - \ln [A]_0 = -\ k \cdot t_{1/2}$$
y nos queda que:
$$t_{1/2} = \frac{-\ \ln 2}{-\ k} = \frac{\ln 2}{k}$$
- Detalles
- Escrito por: Jordi
- Categoría: Cinética química
- Visto: 34874
En una reacción de primer orden, la velocidad de reacción es directamente proporcional a la concentración de una única especie $A$ y es independiente de las concentraciones de todas las demás. Por lo tanto, la ecuación de la velocidad de reacción será:
$$-\ \frac{d[A]}{dt} = k \cdot [A]$$
donde k es el coeficiente de velocidad específica. Existen muchas reacciones que siguen este tipo de comportamiento. Entre ellas son frecuentes las descomposiciones y las isomerizaciones.
Para obtener la ecuación que nos permite saber cómo varía la concentración de $A$ con el tiempo, hemos de integrar la expresión inicial. Tendremos que separar variables primero:
$$-\ \frac{d[A]}{dt} = k \cdot [A]\ \ \Rightarrow\ \ -\ \frac{d[A]}{[A]} = k \cdot dt$$
y ahora integramos:
$$-\ \int_{[A]_0}^{[A]} \frac{d[A]}{[A]} = k \cdot \int_0^t dt$$
$$-\ \left ( {\ln [A] - \ln [A]_0} \right ) = k \cdot t$$
$$\ln {\frac{[A]}{[A]_0}} = -\ k \cdot t$$
$$[A] = [A]_0 \cdot e^{-\ k\cdot t}$$
- Detalles
- Escrito por: Jordi
- Categoría: Cinética química
- Visto: 21194
Hay dos tipos principales de reacciones de segundo orden sencillas. La forma más simple es aquella en la que la velocidad de reacción es proporcional al cuadrado de la concentración de una sola especie de las que intervienen en la reacción. Es decir, cuando la ecuación de la velocidad es de la forma:
$$\displaystyle v = k \cdot [A]^2$$
La otra posibilidad es que la velocidad de reacción sea proporcional al producto de las concentraciones de dos especies. O sea:
$$\displaystyle v = k \cdot [A] \cdot [B]$$
de manera que se trata de una reacción de primer orden respecto a cada una de las dos especies. Vamos a analizar los dos casos.
-
Un ejemplo del primer tipo de reacción de segundo orden es la descomposición térmica del acetaldehído (etanal) gaseoso que, a temperaturas del orden de los 500 ºC, se descompone en metano y monóxido de carbono:
$$\displaystyle CH_{3}\!\!-\!CHO (g)\longrightarrow CH_4 (g) + CO (g)$$
Para esta reacción, se sabe que:
$$\displaystyle v = k \cdot [CH_{3}\!\!-\!CHO]^2$$
- Detalles
- Escrito por: Germán Fernández
- Categoría: Cinética química
- Visto: 3678
Para una reacción reversible $A\rightleftharpoons C$ de primer orden, con constantes cinéticas para la reacción directa $k_1$ e inversa $k{-1}$, determinaremos $[A]$ y $[C]$ en función del tiempo, suponiendo que $[C]_0=0$. La variación de la $[A]$ en el tiempo viene dada por la expresión: \begin{equation}\label{1} \frac{d[A]}{dt}=-k_1[A]+k_{-1}[C] \end{equation} De la estequiometría deducimos, $[C]=[A]_0 -[A]$, sustituyendo en $(\ref{1})$ \begin{equation} \frac{d[A]}{dt}=-k_1[A]+k_{-1}\left([A]_0 - [A]\right) \end{equation}
- Detalles
- Escrito por: Germán Fernández
- Categoría: Cinética química
- Visto: 2543
Sean las reacciones competitivas $A \stackrel{k_1}{\rightarrow}B$ y $A \stackrel{k_2}{\rightarrow}C$ de primer orden, determinaremos $[A]$, $[B]$ y $[C]$ en función del tiempo, suponiendo que $[B]_0=[C]_0=0$. La variación de la $[A]$ en el tiempo viene dada por la expresión: \begin{equation}\frac{d[A]}{dt}=-k_1[A]-k_2[A]\;\;\rightarrow \frac{d[A]}{dt}=(-k_1-k_2)[A]\end{equation}
- Detalles
- Escrito por: Germán Fernández
- Categoría: Cinética química
- Visto: 3385
Sean las reacciones consecutivas $A \stackrel{k_1}{\rightarrow}B\stackrel{k_2}{\rightarrow}C$, de primer orden, determinaremos $[A]$, $[B]$ y $[C]$ en función del tiempo, suponiendo que $[B]_0 =[C]_0=0$. La variación de la $[A]$ en el tiempo viene dada por la expresión: \begin{equation} \frac{d[A]}{dt}=-k_1[A]\label{eq:1} \end{equation} Separando variables e integrando: \begin{equation} [A]=[A]_0 e^{-k_1 t}\label{eq:2} \end{equation} Pasamos ahora a obtener la variación de $[B]$ con t \begin{equation} \frac{d[B]}{dt}=k_1[A]-k_2[B] \end{equation} Sustituyendo $[A]$ por $(\ref{eq:2})$ \begin{equation} \frac{d[B]}{dt}=k_1[A]_0 e^{-k_1 t}-k_2[B] \end{equation}
- Detalles
- Escrito por: Germán Fernández
- Categoría: Cinética química
- Visto: 2512
Obtener la ecuación cinética para la reacción radicalaria en cadena lineal, $H_2 + Br_2 \rightarrow 2HBr$, que transcurre a través del siguiente mecanismo: \begin{eqnarray} Br_2 + M & \stackrel{k_i}{\rightarrow} & 2Br + M\\ Br + H_2 & \stackrel{k_{p1}}{\rightarrow} & HBr + H\\ H + Br_2 & \stackrel{k_{p2}}{\rightarrow} & HBr + Br\\ H + HBr & \stackrel{k_{r}}{\rightarrow} & H_2 + Br\\ 2Br + M & \stackrel{k_{t}}{\rightarrow} & Br_2 + M \end{eqnarray}
(1) Etapa de iniciación
(2) y (3) Etapas de propagación
(4) Etapa de retardo
(5) Etapa de terminación
Lee más: Cinética de las reacciones radicalarias en cadena lineal
- Detalles
- Escrito por: Germán Fernández
- Categoría: Cinética química
- Visto: 5689
Las enzimas son proteínas con pesos moleculares del orden de 104 a 106 y catalizan la mayor parte de las reacciones que ocurren en los seres vivos. La acción de las enzimas es muy específica, catalizando sólo cierta clase de reacciones. Además, concentraciones muy pequeñas de enzima suelen ser suficientes para producir una actividad catalítica enorme sobre grandes cantidades de sustrato. Se denomina sustrato a la molécula sobre la que actúa la enzima. El sustrato se une al centro activo de la enzima, formando el complejo enzima-sustrato. En este complejo el sustrato se transforma en el producto, momento en el cual se libera de la enzima. Existen muchos mecanismos para explicar la catálisis enzimática, aquí consideraremos el más sencillo, el mecanismo de Michaelis Menten, que es: \begin{equation} E+S\rightleftharpoons ES \rightarrow E+P \end{equation} Donde E representa la enzima, S el sustrato, ES el complejo enzima-sustrato y P el producto final. La velocidad de la reacción vendrá dada por la expresión, $r=\frac{d[P]}{dt}=k_2[ES]$
- Detalles
- Escrito por: Germán Fernández
- Categoría: Cinética química
- Visto: 2545
En disoluciones ideales se utiliza como unidad de concentración la molaridad [], mol/l. Si la disolución es real, es necesario utilizar actividades. Tan sólo es necesario sustituir en las ecuaciones la concentración molar por la actividad.\\ Sea la reacción elemental, $aA+bB\rightleftharpoons cC+dD$, la velocidad de la reacción directa en función de actividades viene dada por la ecuación, $r_d=k_da_{A}^{a}a_{B}^{b}$ y la velocidad de la reacción inversa por, $r_i=k_ia_{C}^{c}a_{D}^{d}$.
- Detalles
- Escrito por: Germán Fernández
- Categoría: Cinética química
- Visto: 2473
Octave permite resolver las ecuaciones de un sistema cinético, de forma muy sencilla y eficaz. Aplicaremos Octave a dos sistemas cinéticos complejos: reacciones consecutivas y reacciones oscilantes (mecanismo de Lotka)
a) Reacciones consecutivas:
$A\stackrel{k_1}{\rightarrow} B \stackrel{k_2}{\rightarrow} C$, resolvemos con Octave las siguientes ecuaciones diferenciales: \begin{eqnarray} \frac{d[A]}{dt}& = & -k_1[A]\\ \frac{d[B]}{dt}& = & k_1[A]-k_2[B]\\ \frac{d[C]}{dt}& = & k_2[B] \end{eqnarray}
Creamos una función que proporcione la velocidad de los tres componentes en función de las concentraciones:
octave> function xdot = f(x,t) # x representa las concentraciones de A, B y C, t es el tiempo en un instante dado y xdot son las derivadas de [A], [B] y [C] respecto al tiempo.
> global k # k es un vector que representa las constantes cinéticas $k_1$ y $k_2$ se define de forma global para que sea visible en la función anterior.
> xdot(1) = -k(1)*x(1); # define la primera ecuación
> xdot(2) = k(1)*x(1) - k(2)*x(2); # define la segunda ecuación
> xdot(3) = k(2)*x(2); # define la tercera ecuación.
> endfunction
- Detalles
- Escrito por: Germán Fernández
- Categoría: Cinética química
- Visto: 3423
Para una reacción de primer orden $aA \rightarrow P$, escribimos, \begin{equation} \frac{d[A]}{dt}=-k_A[A] \end{equation} Esta ecuación diferencial es muy sencilla de resolver, pero, supongamos que desconocemos su solución. El método de Euler consiste en aproximar, para un intervalo pequeño de tiempo, las diferenciales por incrementos. \begin{equation} \frac{\Delta [A]}{\Delta t}=-k_A[A]\;\;\;\; \Rightarrow \Delta [A]=-k_A[A]\Delta t \end{equation} Sustituyendo los incrementos por dos concentraciones próximas en el tiempo $[A]_n$ a tiempo $t$ y $[A]_{n+1}$ a tiempo $t_{n+1}$, nos da: \begin{equation} [A]_{n+1}-[A]_{n}=-k_A(t_{n+1}-t_n) \end{equation} Esta última ecuación representa la recta tangente a la curva de [A] vs t en el punto $[A]_n, t_n$.
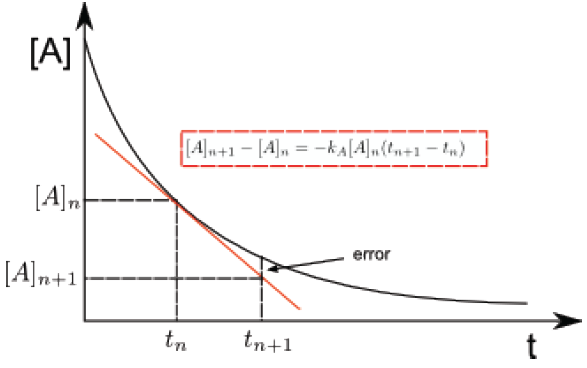
Lee más: Integración numérica de datos cinéticos. Método de Euler
- Detalles
- Escrito por: Germán Fernández
- Categoría: Cinética química
- Visto: 3408
La Ley de Arrhenius se obtiene a partir de la Ley de Van't Hoff. \begin{equation} \frac{dlnkº}{dT}=\frac{\Delta Hº}{RT^2} \end{equation} Cambiando el incremento de entalpía por la energía de activación y la constante de equilibrio por la cinética, se obtiene: \begin{equation} \frac{dlnk}{dT}=\frac{E_a}{RT^2}\label{23} \end{equation} Separando variables e integrando de forma indefinida \begin{equation} \int dlnk=\int\frac{E_a}{RT^2}dT \;\rightarrow \; \; lnk=-\frac{Ea}{RT}+C \end{equation} Llamando lnA a la constante C y despejando k se obtiene: \begin{equation} k=Ae^{-E_a /RT} \end{equation}
- El factor preexponencial, A, representa la frecuencia de colisiones.
- $e^{-E_a /RT}$ representa la fracción de colisiones que son reactivas.
- Detalles
- Escrito por: Germán Fernández
- Categoría: Cinética química
- Visto: 2455
Existen reacciones en las que la concentración de un reactante aumenta y disminuye con el tiempo de forma periódica. Este tipo de comportamiento está asociado a etapas autocatalíticas. En 1920 A. J. Lotka propuso un sencillo mecanismo en el que las concentraciones de los componentes X e Y oscilan periódicamente. El mecanismo de Lotka es el siguiente: \begin{equation} A+X\stackrel{k_1}{\rightarrow} 2X \end{equation} \begin{equation} X+Y\stackrel{k_2}{\rightarrow} 2Y \end{equation} \begin{equation} Y\stackrel{k_3}{\rightarrow} B \end{equation} El comportamiento oscilante de este sistema se observa si la concentración de A se mantiene constante, por tanto, es necesario añadir A al mismo ritmo que se gasta.
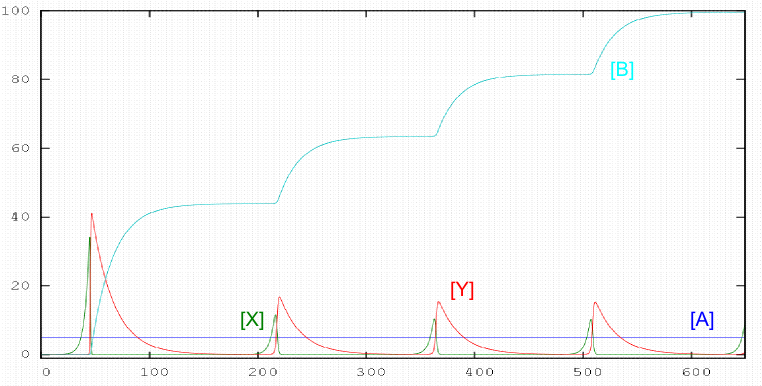
- Detalles
- Escrito por: Germán Fernández
- Categoría: Cinética química
- Visto: 4009
Un ejemplo muy sencillo de autocatálisis lo encontramos en la siguiente reacción: \begin{equation} A+B\stackrel{k}{\rightarrow}2B \;\; \Rightarrow r=-\frac{dA}{dt}=k[A][B] \end{equation} En los instantes iniciales se produce un aumento en la concentración de B, que origina un rápido incremento en la velocidad (obsérvese que B es reactivo y producto). Sin embargo, a medida que transcurre la reacción va desapareciendo el reactivo A y la velocidad empieza a disminuir, hasta hacerse nula, cuando desaparezca este componente. La evolución de las concentraciones de A y B con el tiempo, es una curva sigmoide, que responde a la siguiente ecuación: \begin{equation} kt=\frac{1}{[A]_0+[B]_0}ln\frac{[B]/[B]_0}{[A]/[A]_0} \end{equation}

- Detalles
- Escrito por: Germán Fernández
- Categoría: Cinética química
- Visto: 3089
Método del flujo rápido
Muchas reacciones son demasiado rápidas para ser estudiadas mediante métodos clásicos. Se pueden emplear métodos de flujo rápido para su estudio.
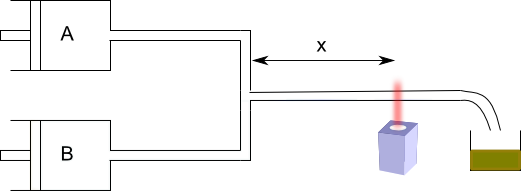
Este sistema permite medir [A] para tiempos pequeños. El método de flujo rápido permite estudiar reacciones con semividas comprendidas entre 10 y $10^{-3}$ segundos. La mayor limitación de las técnicas de flujo rápido es el tiempo de mezcla de los reactivos. Métodos más efectivos para determinar estas cinéticas, son los métodos de relajación. En ellos se parte de un sistema reactivo en equilibrio, se cambia bruscamente alguna variable (T,P, ect.) y se estudia el retorno del sistema al nuevo equilibrio, pudiendo determinarse las constantes cinéticas.
- Detalles
- Escrito por: Germán Fernández
- Categoría: Cinética química
- Visto: 3121
Se cree que los pasos más importantes de la reacción $2H_2+O_2 \rightarrow H_2O$ corresponden a una reacción en cadena ramificada, con etapas elementales: \begin{eqnarray} H_2 & \rightarrow & 2H\\ H_2+OH & \rightarrow & H + H_2O\\ H + O_2 & \rightarrow & OH + O\\ O + H_2 & \rightarrow & OH + H\\ 2H + pared & \rightarrow & H_2\\ H+O_2+M & \rightarrow & HO_2 + M^{\ast} \end{eqnarray} El radical $HO_2$ es de larga vida, y los radicales O y OH son mucho más reactivos que el H.
1. Identifica las etapas de iniciación, propagación, ramificación y terminación.
2. Muestra que, del balance de las etapas de propagación y ramificación, el resultado es la reacción global más una generación de radicales neta.
3. Aplica la hipótesis de estado estacionario a las concentraciones de los radicales libres O y OH para hallar sus concentraciones en función de la de H (más abundante).
4. Considerando que la etapa 5 es de orden 1 (controlada por la adsorción y difusión en las paredes) y la etapa 1 es de orden cero (producida a ritmo constante por circunstancias externas), encuentra la ecuación diferencial que gobierna la generación de radicales H.
5. La solución de la ecuación diferencial tiene dos regímenes, en función del signo de b. Discute las condiciones en las que se da cada uno de esos regímenes, y su significado.
- Detalles
- Escrito por: Germán Fernández
- Categoría: Cinética química
- Visto: 2688
La velocidad de una reacción puede depender fuertemente del disolvente. Como ejemplo, sea la $S_N2$: $CH_3I + Cl^- \rightarrow CH_3Cl + I^-$, la velocidad depende del disolvente ya que este cambia el valor de k, debido a la distinta solvatación de los reactivos. En otras ocasiones, reacciones muy rápidas se ven limitadas por la velocidad de difusión de los reactivos a través del disolvente (viscosidad del disolvente). El valor de k también depende de los puentes de hidrógeno. Una reacción que puede transcurrir a través de dos mecanismos competitivos, las velocidades pueden verse afectadas y seguir un mecanismo en un disolvente y el otro en otro disolvente diferente.
Encuentros, colisiones y el efecto de celda
En un gas las moléculas están distantes y se mueven libremente. En un líquido, una molécula se encuentra rodeada por otras moléculas "celda de disolvente". Esta molécula choca contra las paredes de la celda antes de poder escapar.