Termodinámica estadística
- Detalles
- Escrito por: Germán Fernández
- Categoría: Termodinámica estadística
- Visto: 2328
La mecánica estadística es la parte de la química física que permite la predicción de propiedades termodinámicas a partir de los datos proporcionados por la mecánica cuántica. Así, a partir de propiedades microscópicas de la materia (cuánticas) se pueden obtener propiedades macroscópicas como entropía, capacidades caloríficas, energía interna , tensión superficial, viscosidad,....
La termodinámica estadística supone que la materia está formada por un elevado número de componentes microcópicos que individualmente obedecen a la mecánica cuántica, pero como colectivo obedecen las leyes estadísticas. La termodinámica estadística establece una conexión entre la descripción microcópica y la descripción macroscópica de la naturaleza.
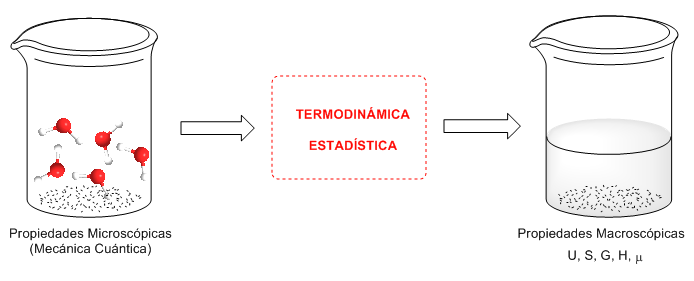
Basándose en los resultados a nivel molecular que se obtienen con la mecánica cuántica, la termodinámica estadística calcula propiedades directamente observables.
- Detalles
- Escrito por: Germán Fernández
- Categoría: Termodinámica estadística
- Visto: 4149
Las partículas cumplen tres condiciones:
- Son distinguibles entre si (este hecho afecta a la entropía)
- Cumplen las leyes de la mecánica cuántica.
- Además, no interaccionan unas con otras.
- Detalles
- Escrito por: Germán Fernández
- Categoría: Termodinámica estadística
- Visto: 3320
Calculemos ahora el número de microestados asociados a una distribución cualquiera. Sean N partículas distinguibles distribuidas en \(r\) estados cuánticos, como sigue: \(N_{1}\) partículas en \(\epsilon_{1}\), \(N_{2}\) en \(\epsilon_2\),........,\(N_r\) en \(\epsilon_r\). El número de microestados de este macroestado viene dado por la ecuación:.![]()
- Detalles
- Escrito por: Germán Fernández
- Categoría: Termodinámica estadística
- Visto: 2360
La probabilidad de que un sistema se encuentre en una cierta distribución será tanto mayor cuanto mayor sea el número de microestados asociados a la distribución. Sea \(W_i\) el número de microestados asociados a una cierta distribución \(i\), la probabilidad de que el sistema se halle en dicha distribución será: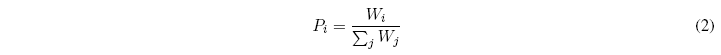
- Detalles
- Escrito por: Germán Fernández
- Categoría: Termodinámica estadística
- Visto: 2855
Vamos a calcular de entre todos los macroestados posibles del sistema aquel que posee el mayor número de microestados. Así, el cálculo de cualquier magnitud termodinámica se realiza despreciando todos los macroestados excepto el más probable. Matemáticamente debemos calcular $N_{1},N_{2},.....,N_{r}$ de modo que W tome el valor máximo. Donde W viene dado por: \begin{equation} W=N!\prod_{k}\frac{g_{k}^{N_{k}}}{N_{k}!} \label{ec3} \end{equation} Tomando neperianos en (\ref{ec3}) \begin{equation} lnW=lnN!+\sum\left(N_{k}lng_{k}-lnN_{k}!\right) \label{ec4} \end{equation} Aplicando en (~\ref{ec4}) la aproximación de Stirling $lnN!=NlnN-N$: \begin{equation} lnW=NlnN-N+\sum_{k}N_{k}lng_{k}-\sum_{k}\left(N_{k}lnN_{k}-N_{k}\right) \label{ec5} \end{equation}
Lee más: Distribución más probable: Ley de distribución de Boltzmann
- Detalles
- Escrito por: Germán Fernández
- Categoría: Termodinámica estadística
- Visto: 3345
Boltzmann postuló la existencia de una relación entre la entropía total de un sistema termodinámico y el número total de microestados $(\Omega)$ en los que puede hallarse el sistema. \begin{equation} S=kln\Omega \label{ec17} \end{equation} Como $\Omega=\sum_{j}W_{j}\approx{W_{max}}$, donde $W_{max}$ representa al macroestado más probable, que por simplicidad representaremos por $W$. Así, el Postulado de Boltzmann nos queda: \begin{equation} S=klnW \label{ec18} \end{equation} donde $k$ es la constante de Boltzmann $k=1,38\cdot10^{-27}J/K$ y $W$ es el macroestado con mayor número de microestados.
- Detalles
- Escrito por: Germán Fernández
- Categoría: Termodinámica estadística
- Visto: 1868
\begin{equation} E=\sum_{i}N_{i}\epsilon_{i}=\sum_{i}\frac{N}{q}g_{i}e^{-\beta{\epsilon_{i}}}\epsilon_{i}=\frac{N}{q}\sum_{i}g_{i}\epsilon_{i}e^{-{\epsilon_{i}}/kT} \label{ec31} \end{equation} Derivando $q=\sum_{i}g_{i}e^{-\epsilon_{i}/kT}$ respecto de $T$ a volumen: \begin{equation} \left(\frac{\partial{q}}{\partial{T}}\right)_{V}=\frac{1}{kT^2}\sum_{i}g_{i}\epsilon_{i}e^{-\epsilon_{i}/kT} \label{ec32} \end{equation} Despejando el sumatorio de la ecuación (~\ref{ec32}): \begin{equation} kT^{2}\left(\frac{\partial{q}}{\partial{T}}\right)_{V}=\sum_{i}g_{i}\epsilon_{i}e^{-\epsilon_{i}/kT} \label{ec33} \end{equation} Sustituyendo (~\ref{ec33}) en (~\ref{ec31}) \begin{equation} E=NkT^{2}\left(\frac{\partial{lnq}}{\partial{T}}\right)_{V} \label{ec34} \end{equation}
- Detalles
- Escrito por: Germán Fernández
- Categoría: Termodinámica estadística
- Visto: 1962
Partimos de la expresión termodinámica para la energía libre de Helmholtz: \begin{equation} A=E-TS \label{ec35} \end{equation} Sustituyendo $S$ por su valor: \begin{equation} A=E-T\left(\frac{E}{T}+Nklnq\right)=-NkTlnq \label{ec36} \end{equation} Así, la ecuación de Helmholtz en mecánica estadística nos queda: \begin{equation} A=-NkTlnq \label{ec37} \end{equation}
- Detalles
- Escrito por: Germán Fernández
- Categoría: Termodinámica estadística
- Visto: 1941
Como $dA=-SdT-PdV$
a $T=cte$
nos da $P=-\left(\frac{\partial{A}}{\partial{V}}\right)_{T=cte}$
Derivando la ecuación $A=-NkTlnq$ respecto del volumen y sustituyendo en P, nos da: \begin{equation} P=NkT\left(\frac{\partial{lnq}}{\partial{V}}\right)_{T=cte} \label{ec38} \end{equation}
- Detalles
- Escrito por: Germán Fernández
- Categoría: Termodinámica estadística
- Visto: 2040
Consideremos ahora la función de partición molecular $q=\sum_{i}g_{i}e^{-\beta{\epsilon_{i}}}$. La energía molecular es suma de energía traslacional, rotacional, vibracional y electrónica. \begin{equation} \epsilon_{i}=\epsilon_{tr,n}+\epsilon_{vib,v}+\epsilon_{rot,J}+\epsilon_{ele,u} \label{ec39} \end{equation} Sustituyendo en la función de partición molecular $q$ \begin{equation} q={\sum{g_{i}}{e^{-\beta\left(\epsilon_{tr,n}+\epsilon_{vib,v}+\epsilon_{rot,J}+\epsilon_{ele,u}\right)}}=\sum_{n}g_{n}e^{-\beta{\epsilon_{tr,n}}}\sum_{v}g_{v}e^{-\beta{\epsilon_{vib,v}}}\sum_{J}g_{J}e^{-\beta{\epsilon_{rot,J}}}\sum_{u}g_{u}e^{-\beta{\epsilon_{ele,u}}}} \label{ec40} \end{equation} \begin{equation} q=q_{tr}\cdot{q_{vib}}\cdot{q_{rot}}\cdot{q_{ele}} \label{ec41} \end{equation}
- Detalles
- Escrito por: Germán Fernández
- Categoría: Termodinámica estadística
- Visto: 2373
Los niveles de energía traslacionales vienen dados por el modelo de la partícula en una caja tridimensional. \begin{equation} \epsilon_{tr}=\frac{h^2}{8m}\left(\frac{n_{x}^{2}}{a^2}+\frac{n_{y}^{2}}{a^2}+\frac{n_{z}^{2}}{a^2}\right) \end{equation} \begin{equation} q_{tr}=\sum e^{\beta\epsilon_{tr}}=\sum e^{\frac{\beta h^2}{8m}\left(\frac{n_{x}^{2}}{a^2}+\frac{n_{y}^{2}}{a^2}+\frac{n_{z}^{2}}{a^2}\right)}=\sum_{n_x =1}^{\infty}e^{-\frac{\beta h^2n_{x}^{2}}{8ma^2}}\sum_{n_y =1}^{\infty}e^{-\frac{\beta h^2n_{y}^{2}}{8mb^2}}\sum_{n_z =1}^{\infty}e^{-\frac{\beta h^2n_{z}^{2}}{8mc^2}} \end{equation}
- Detalles
- Escrito por: Germán Fernández
- Categoría: Termodinámica estadística
- Visto: 2022
A partir de la función de partición traslacional se puede obtener la presión de un gas ideal. \begin{equation} P=NKT\left(\frac{\partial lnq_{tr}}{\partial V}\right)_T \end{equation} Escribimos la función de partición traslacional: \begin{equation} q_{tr}=\left(\frac{2\pi mkT}{h^2}\right)^{3/2}V \end{equation} Tomando logaritmos neperiano \begin{equation} lnq_{tr}=ln\left(\frac{2\pi mkT}{h^2}\right)^{3/2}+lnV \end{equation}
- Detalles
- Escrito por: Germán Fernández
- Categoría: Termodinámica estadística
- Visto: 2548
La energía de los diferentes niveles rotacionales vienen dados por el modelo del rotor rígido: $\epsilon_{rot,J}=\frac{\hbar^2J(J+1)}{2I}$, la degeneración de los niveles es $g_J=2J+1$ \begin{equation} q_{rot}=\sum_{J=0}^{\infty}g_Je^{\epsilon_{rot,J}/kT}=\sum_{J=0}^{\infty}(2J+1)e^{-\frac{\hbar^2 J(J+1)}{2IkT}} \end{equation} Llamamos temperatura rotacional $\theta_{rot}$ a: $\theta_{rot}=\frac{\hbar^2}{2Ik}$, tiene unidades de temperatura (K) pero no es temperatura en sentido físico.
- Detalles
- Escrito por: Germán Fernández
- Categoría: Termodinámica estadística
- Visto: 2575
La aproximación del oscilador armónico da $\epsilon_{vib}=\left(v+\frac{1}{2}\right)h\nu$ donde $v$ es el número cuantico vibracional que oscila entre $[0,\infty]$ y no hay degeneración.
Es usual en mecánica estadística tomar el nivel más bajo de energía como cero $\epsilon_{vib}=\left(v+\frac{1}{2}\right)h\nu-\frac{1}{2}h\nu=vh\nu$
- Detalles
- Escrito por: Germán Fernández
- Categoría: Termodinámica estadística
- Visto: 2245
Calculamos $q_{ele}$ como una suma extendida a los niveles de energía electrónicos, por lo que incluiremos la degeneración $g_{ele}$ de cada nivel. \begin{equation} q_{ele}=\sum_{i}g_{ele,i}e^{-\frac{\epsilon_{ele,i}}{k T}}=g_{ele,0}+g_{ele,1}e^{-\frac{\epsilon_{ele,1}}{k T}}+g_{ele,2}e^{-\frac{\epsilon_{ele,2}}{k T}}+.... \end{equation} En esta última ecuación hemos tomado como cero la energía electrónica del nivel fundamental
- Detalles
- Escrito por: Germán Fernández
- Categoría: Termodinámica estadística
- Visto: 2102
\begin{equation} E=E_{tr}+E_{rot}+E_{vib}+E_{ele} \end{equation} Cálculo de la energía interna traslacional \begin{equation} E_{tr}=NkT^2\left(\frac{\partial lnq_{tr}}{\partial T}\right)_{V} \end{equation} \begin{equation} q_{tr}=\left(\frac{2\pi mkT}{h^2}\right)^{3/2}V \Rightarrow lnq_{tr}=\frac{3}{2}lnT+ln\left(\frac{2\pi mk}{h^2}\right)_V \end{equation}



