Segundo principio | Termodinámica
- Detalles
- Escrito por: Germán Fernández
- Categoría: Segundo principio de la Termodinámica
- Visto: 1927
El segundo principio de la termodinámica establece el sentido de los procesos físicos espontáneos. Introduce una nueva magnitud denominada entropía, que tiende a aumentar su valor en todo proceso termodinámico irreversible que se realice en un sistema aislado.
- Detalles
- Escrito por: Germán Fernández
- Categoría: Segundo principio de la Termodinámica
- Visto: 4588
Enunciado de Kelvin-Planck, es imposible que un sistema realice un proceso cíclico cuyos únicos efectos sean el flujo de calor desde una fuente de calor al sistema y la realización, por parte del sistema, de una cantidad equivalente de trabajo.

- Detalles
- Escrito por: Germán Fernández
- Categoría: Segundo principio de la Termodinámica
- Visto: 2864
Una máquina térmica es un dispositivo de funcionamiento cíclico que absorbe una cantidad de calor de un foco caliente (por ejemplo, la caldera), realiza un trabajo -w sobre los alrededores, y cede una cantidad de calor a un foco frío.

El rendimiento o eficacia de una máquina térmica es la fracción de energía suministrada que se convierte en trabajo. La máquina consume por ciclo una energía \(q_c\) y realiza un trabajo \(-w\), así que el rendimiento será:
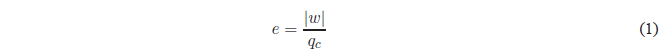
- Detalles
- Escrito por: Germán Fernández
- Categoría: Segundo principio de la Termodinámica
- Visto: 1878
"Ninguna máquina térmica puede ser más eficiente que una máquina térmica reversible, cuando ambas máquinas trabajan entre el mismo par de temperaturas". Para una misma cantidad de calor absorbido, la máquina reversible genera la máxima cantidad de trabajo.
- Detalles
- Escrito por: Germán Fernández
- Categoría: Segundo principio de la Termodinámica
- Visto: 1867
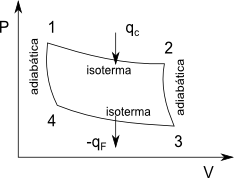
Es un ciclo reversible que consta de dos etapas isotérmicas a diferente temperatura y dos etapas adiabáticas. La sustancia de trabajo puede no ser un gas ideal, pero en este desarrollo por simplicidad usaremos un mol de gas ideal.
- Detalles
- Escrito por: Germán Fernández
- Categoría: Segundo principio de la Termodinámica
- Visto: 2664
Ahora calculemos el rendimiento de un ciclo de Carnot, usando como sustancia de trabajo un mol de gas ideal y con sólo trabajo P-V.
Escribimos la ecuación del primer principio: \begin{equation} dU=dq+dw=dq-pdV \end{equation} Para un gas ideal se cumple que: \begin{equation} dU=C_vdT\;\;y\;\;P=\frac{nRT}{V} \end{equation} Sustituyendo en el primer principio: \begin{equation} C_vdT=dq-\frac{nRT}{V}dV \end{equation} Dividiendo toda la ecuación por T \begin{equation} \frac{C_v}{T}dT=\frac{dq}{T}-nR\frac{dV}{V} \end{equation} Integrando sobre el ciclo de Carnot \begin{equation} \oint C_v\frac{dT}{T}=\oint\frac{dq}{T}-nR\oint\frac{dV}{V} \end{equation} Las integrales $\oint C_v\frac{dT}{T}$ y $\oint\frac{dV}{V}$ son cero ya que los integrandos son diferenciales de funciones de estado y la integral a lo largo de un ciclo es cero.
- Detalles
- Escrito por: Germán Fernández
- Categoría: Segundo principio de la Termodinámica
- Visto: 2976
La entropía es una función de estado descubierta por Clausius en 1854 y definida por la siguiente expresión: \begin{equation} dS=\frac{dq}{T} \end{equation} El cambio de entropía entre dos estados 1 y 2 se obtiene integrando la expresión diferencial: \begin{equation} \Delta S=\int_{1}^{2}\frac{dq}{T} \end{equation} La entropía es una medida del desorden que posee un sistema. Cuanto más desordenado sea, mayor entropía posee.
Así, el agua sólida (moléculas ordenadas) tiene menos entropía que el agua líquida (moléculas con libertad de movimiento).
La entropía también nos indica la dirección que siguen los procesos espontáneos. Supongamos un recipiente dividido por una pared que contiene a un lado nitrógeno y a otro oxígeno, quitamos la pared y los gases se mezclan espontáneamente. Las moléculas nitrógeno y oxígeno difunden por todo recipiente obteniéndose al cabo de un cierto tiempo una mezcla perfecta de ambos gases.
- Detalles
- Escrito por: Germán Fernández
- Categoría: Segundo principio de la Termodinámica
- Visto: 2310
Proceso cíclico
El cambio de entropía en un proceso cíclico es cero. Los estados inicial y final coinciden. \begin{equation} \Delta S=\oint\frac{dq}{T}=0 \end{equation}
Proceso adiabático reversible.
En un proceso adiabático no se intercambia calor entre el sistema y el entorno $dq_{rev}=0$ \begin{equation} \Delta S=\int\frac{dq_{rev}}{T}=0 \end{equation}
Cambio de fase reversible a T y P constantes.
Un cambio de fase tiene lugar a temperatura y presión constantes. La temperatura sale fuera de la integral y el calor intercambiado en el cambio de fase es igual a la variación de entalpía. \begin{equation} \Delta S=\int_{1}^{2}\frac{dq_{rev}}{T}=\frac{1}{T}\int_{1}^{2}dq_{rev}=\frac{q_{rev}}{T}=\frac{\Delta H}{T} \end{equation}
Lee más: Cálculo de variaciones de entropía en algunos sistemas típicos
- Detalles
- Escrito por: Germán Fernández
- Categoría: Segundo principio de la Termodinámica
- Visto: 2315
En las secciones anteriores hemos considerado los cambios de entropía en el sistema para los procesos más típicos. Ahora estudiaremos las variaciones de entropía que ocurren en el sistema y en el entorno. Llamamos universo al conjunto de sistema más entorno que interacciona con él. \begin{equation} \Delta S_{uni}=\Delta S_{sis}+\Delta S_{ent} \end{equation}
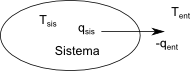
Calculemos la variación de entropía que sufre el universo en un proceso reversible. Supongamos que se produce un flujo infinitesimal de calor dq desde el sistema hacia el entorno. Para que el proceso sea reversible es necesario que la diferencia de temperatura entre el sistema y el entorno sea un dT, de lo contrario el proceso será irreversible. \begin{equation} dS_{uni}=dS_{sis}+dS_{ent}=\frac{dq_{sis}}{T_{sis}}+\frac{dq_{ent}}{T_{ent}} \end{equation} El calor que recibe el sistema es igual al que cede el entorno, $q_{sis}=-q_{ent}$ y las temperaturas sólo se diferencian en una cantidad infinitesimal,$T_{sis}=T_{ent}$ , por lo que podemos considerarlas iguales. \begin{eqnarray} dS_{uni} & = & \frac{dq_{sis}}{T_{sis}}+\frac{-dq_{sis}}{T_{sis}}=0\\ \Delta S_{uni} & = & 0 \end{eqnarray}
- Detalles
- Escrito por: Germán Fernández
- Categoría: Segundo principio de la Termodinámica
- Visto: 3535
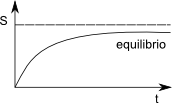
Un sistema termodinámico aislado alcanza el equilibrio cuando la entropía del sistema es máxima. Por ejemplo, el flujo de calor desde un cuerpo caliente a otro frío suponen un incremento de entropía. Este aumento tiene lugar hasta que los cuerpos alcanzan la misma temperatura (equilibrio térmico). El proceso de disolución de una sal en agua suponen un incremento de entropía, que cesa cuando toda la sal se ha disuelto.
- Detalles
- Escrito por: Jordi
- Categoría: Segundo principio de la Termodinámica
- Visto: 4244
Hay una forma de entender los procesos irreversibles que siempre me ha hecho mucha gracia: supongamos que ponemos arena de dos colores en un recipiente. Primero colocamos en el fondo la de color 1. Luego, encima, se vierte la de color 2. Claramente, la arena está ordenada, cada color en su sitio. Ahora, cogemos una varilla o un palo y vamos removiendo en el sentido de las agujas del reloj. Al cabo de un cierto tiempo, toda la arena se habrá ido mezclando y será imposible distinguir los dos colores: ahora sólo queda un único color más o menos uniforme. Si este proceso de mezcla fuese reversible, bastaría con volver a remover la arena con el palo, esta vez girándolo en sentido antihorario, y podríamos ver cómo los colores vuelven a separarse. ¿No es así, verdad? Pues ésto es un ejemplo de proceso irreversible.



