Equilibrio en sistemas de un componente
- Detalles
- Escrito por: Germán Fernández
- Categoría: Equilibrio de fases en sistemas de un componente
- Visto: 3294
La regla de las fases intenta responder a la pregunta general de cuantas varibles independientes se necesitan para definir el estado de equilibrio de un sistema de fases y componentes múltiples.
Definimos el número de grados de libertad (f) de un sistema en equilibrio, como el número de variables intensivas independientes que se necesitan para especificar su estado termodinámico.
Inicialmente haremos dos suposiciones, que más tarde se eliminarán:
- No ocurre ninguna reacción química
- Todas las especies químicas están presentes en cada una de las fases.
Sea un sistema formado por c especies químicas diferentes y p fases.
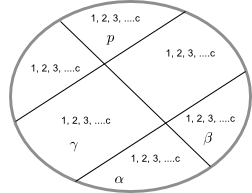
Para dar la composición del sistema necesitamos especificar las fracciones molares de cada componente en cada fase.
Composición de la fase $\alpha$: $x_{1}^{\alpha},x_{2}^{\alpha},x_{3}^{\alpha}, ........, x_{c}^{\alpha}$
Composición de la fase $\beta$: $x_{1}^{\beta},x_{2}^{\beta},x_{3}^{\beta}, ........, x_{c}^{\beta}$
..............................................................................
Composición de la fase $p$: $x_{1}^{p},x_{2}^{p},x_{3}^{p}, ........, x_{c}^{p}$
Necesitamos, por tanto, $c\times p$ fracciones molares.
- Detalles
- Escrito por: Germán Fernández
- Categoría: Equilibrio de fases en sistemas de un componente
- Visto: 2970
Entalpía de fusión ($\Delta \bar{H}_{fus}$), es el calor necesario para pasar un mol de sólido a líquido.
Entalpía de vaporización ($\Delta \bar{H}_{vap}$), es el calor necesario para pasar un mol de líquido a gas.
Entalpía de sublimación ($\Delta \bar{H}_{sub}$), es el calor necesario para pasar un mol de sólido a gas.
En el punto triple se cumple la relación: $\Delta H_{sub}=\Delta H_{fus}+\Delta H_{ebu}$
- Detalles
- Escrito por: Germán Fernández
- Categoría: Equilibrio de fases en sistemas de un componente
- Visto: 3172
La ecuación de Clapeyron nos permite calcular la pendiente de la línea de equilibrio $dP/dT$ a cualquier valor de P,T.
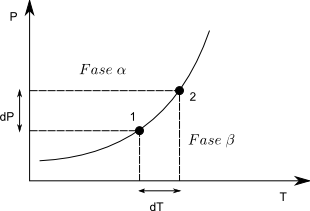
Consideremos dos puntos sobre la línea de equilibrio, en cualquiera de ellos se debe cumplir, $\mu^{\alpha}=\mu^{\beta}$, es innecesario el subíndice por ser una sustancia pura. Como el potencial químico coincide con la energía libre de Gibbs molar $\bar{G}_{1}^{\alpha}=\bar{G}_{1}^{\beta}$. Al pasar del punto (1) al (2) se produce un cambio infinitesimal en G y podemos escribir: \begin{equation} d\bar{G}^{\alpha}=d\bar{G}^{\beta} \end{equation}
- Detalles
- Escrito por: Germán Fernández
- Categoría: Equilibrio de fases en sistemas de un componente
- Visto: 3397
Consideremos un sistema con un sólo componente $(H_2O)$ despreciamos la disociación. Vamos a representar cualquier estado del sistema mediante un diagrama de fases.
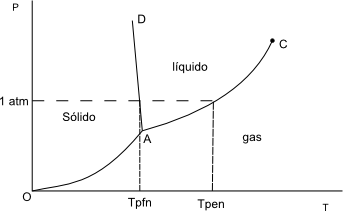
A temperaturas bajas y presiones moderadas o altas tenemos la fase sólida. A presiones bajas la fase gaseosa y a temperaturas y presiones intermedias la fase líquida.



