La ecuación de Clapeyron nos permite calcular la pendiente de la línea de equilibrio $dP/dT$ a cualquier valor de P,T.
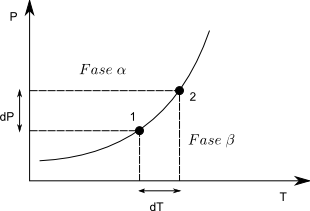
Consideremos dos puntos sobre la línea de equilibrio, en cualquiera de ellos se debe cumplir, $\mu^{\alpha}=\mu^{\beta}$, es innecesario el subíndice por ser una sustancia pura. Como el potencial químico coincide con la energía libre de Gibbs molar $\bar{G}_{1}^{\alpha}=\bar{G}_{1}^{\beta}$. Al pasar del punto (1) al (2) se produce un cambio infinitesimal en G y podemos escribir: \begin{equation} d\bar{G}^{\alpha}=d\bar{G}^{\beta} \end{equation}
Aplicando la expresión, $d\bar{G}=-\bar{S}dT+\bar{V}dP$ a la ecuación anterior se obtiene: \begin{equation} -\bar{S}^{\alpha}dT+\bar{V}^{\alpha}dP= -\bar{S}^{\beta}dT+\bar{V}^{\beta}dP \end{equation} Agrupando términos \begin{equation} (\bar{V}^{\alpha}-\bar{V}^{\beta})dP=(\bar{S}^{\alpha}-\bar{S}^{\beta})dT \end{equation} Despejando \begin{equation} \frac{dP}{dT}=\frac{\bar{S}^{\alpha}-\bar{S}^{\beta}}{\bar{V}^{\alpha}-\bar{V}^{\beta}}=\frac{\Delta S}{\Delta V} \end{equation} $\Delta S$ y $\Delta V$ son los cambios de entropía y volumen al pasar de la fase $\beta$ a la $\alpha$. En caso de ir de la fase $\alpha$ a la $\beta$ cambiarían los signos tanto del numerador como del denominador sin alterar el cociente.
Dado que $\Delta S=\frac{\Delta H}{T}$, la ecuación anterior nos da: \begin{equation} \frac{dP}{dT}=\frac{\Delta H}{T\Delta V} \end{equation} Esta última expresión se conoce como ecuación de Clapeyron.



