Clapeyron's equation allows us to calculate the slope of the equilibrium line $dP/dT$ at any value of P,T.
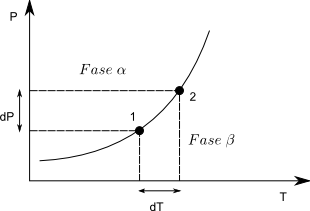
Let us consider two points on the equilibrium line, in any of them it must be fulfilled, $\mu^{\alpha}=\mu^{\beta}$, the subscript is unnecessary because it is a pure substance. As the chemical potential coincides with the Gibbs free energy molar $\bar{G}_{1}^{\alpha}=\bar{G}_{1}^{\beta}$. Going from point (1) to (2) produces an infinitesimal change in G and we can write:
\begin{equation} d\bar{G}^{\alpha}=d\bar{G}^{\beta} \end{equation}
Applying the expression, $d\bar{G}=-\bar{S}dT+\bar{V}dP$ to the previous equation, we obtain:
\begin{equation} -\bar{S}^ {\alpha}dT+\bar{V}^{\alpha}dP= -\bar{S}^{\beta}dT+\bar{V}^{\beta}dP \end{equation}
Grouping
\begin{equation} (\bar{V}^{\alpha}-\bar{V}^{\beta})dP=(\bar{S}^{\alpha}-\bar{S}^{\beta}) dT \end{equation}
Solving for
\begin{equation} \frac{dP}{dT}=\frac{\bar{S}^{\alpha}-\bar{S}^{\beta}}{\bar{ V}^{\alpha}-\bar{V}^{\beta}}=\frac{\Delta S}{\Delta V} \end{equation}
$\Delta S$ and $\Delta V$ are the entropy and volume changes when passing from the $\beta$ to the $\alpha$ phase. In the case of going from the $\alpha$ to the $\beta$ phase, the signs of both the numerator and the denominator would change without altering the quotient.
Since $\Delta S=\frac{\Delta H}{T}$, the above equation gives us:
\begin{equation} \frac{dP}{dT}=\frac{\Delta H}{T\Delta V} \end{equation}
This last expression is known as the Clapeyron equation.



