Rotación vibración en diatómicas
- Detalles
- Escrito por: Germán Fernández
- Categoría: Rotación vibración en moléculas diatómicas
- Visto: 1793
La aproximación de Born-Oppenheimer permite separar la ecuación de Schrodinger para una molécula en una ecuación electrónica y otra nuclear. La ecuación de Schrödinger para el movimiento nuclear en un estado electrónico determinado viene dada por:
\begin{equation}\label{1} \left(\hat{T}_N + E_e\right)\psi_N=E\psi_N \end{equation}
Donde $\hat{T}_N$ representa la energía cinética de los nucleos. $E_e$ es el potencial nuclear (energía electrónica y repulsión entre nucleos) y depende del estado electrónico de la molécula. E es la energía total de la molécula.
Particularizando estos resultados para una molécula diatómica compuesta por dos átomos 1 y 2 de masas $m_1$ y $m_2$
\begin{equation}\label{2} \left[-\frac{\hbar^2}{2m_1}\nabla_{1}^{2}-\frac{\hbar^2}{2m_2}\nabla_{2}^{2} +E_e(R)\right]\psi_N =E\psi_N \end{equation}
- Detalles
- Escrito por: Germán Fernández
- Categoría: Rotación vibración en moléculas diatómicas
- Visto: 2163
La energía cinética del movimiento interno puede separarse en dos energías puede dividirse en energía cinética de rotación y energía cinética de vibración. Inicialmente realizaremos la aproximación de que ambos movimietos son independientes, puesto que el movimiento rotacional depende de los angulos $\theta$ y $\varphi$ mientras que el movimiento vibracional sólo depende de la distancia entre nucleos $R$.
\begin{equation} \frac{-\hbar}{2\mu}\nabla^2\psi_{rot}=E_{rot}\psi_{rot} \end{equation}
El modelo del rotor rígido nos da la energía rotacional de una molécula diatómica:
\begin{equation}\label{4} E_{rot}=\frac{\hbar^2 J(J+1)}{2I_e} \end{equation}
Donde $I_e=\mu R_{e}^{2}$ es el momento de inercia de equilibrio.
- Detalles
- Escrito por: Germán Fernández
- Categoría: Rotación vibración en moléculas diatómicas
- Visto: 2308
La energía vibracional se obtiene resolviendo la ecuación de Schrödinger vibracional
\begin{equation}\label{6} \left[-\frac{\hbar^2}{2\mu}\frac{d^2}{dR^2}+E_e(R)\right]\psi_{vib}(R)=(E_{vib}+E_{ele})\psi_{vib}(R) \end{equation}
El desarrollo en series de Taylor de la energía potencial $E_e(R)$ en torno a la distancia de equilibrio $R_e$ nos da:
\begin{equation}\label{71} E_e(R)\approx E_e(R_e)+\frac{1}{2}\frac{d^2E_e(R_e)}{dR^2}(R-R_e)^2+..... \end{equation}
La cantidad $E_e(R_e)=E_{el}$ es constante para un determinado estado electrónico y se denomina energía electrónica de equilibrio.
- Detalles
- Escrito por: Germán Fernández
- Categoría: Rotación vibración en moléculas diatómicas
- Visto: 1999
La energía obtenida para el oscilador armónico depende del desarrollo (ecuación 2) que se truncó por el segundo término. Añadiendo las derivadas tercera y cuarta el desarrollo se obtiene una mejor aproximación para la energía. El término de corrección para la ecuación de la energía vibracional es: $-h\nu_e x_e(v+\frac{1}{2})^2$, donde $\nu_e x_e$ se conoce como constante de anarmonicidad. La energía vibracional corregida es: $ E_{vib}=(v+\frac{1}{2})h\nu_e-h\nu_e x_e(v+\frac{1}{2})^2$
La inclusión de la anarmonicidad nos deja la energía interna de la molécula como sigue:
\begin{equation}\label{13} E_{int}=B_e h J(J+1)+(v+\frac{1}{2})h\nu_e-h\nu_e x_e(v+\frac{1}{2})^2+E_{ele} \end{equation}
- Detalles
- Escrito por: Germán Fernández
- Categoría: Rotación vibración en moléculas diatómicas
- Visto: 3268
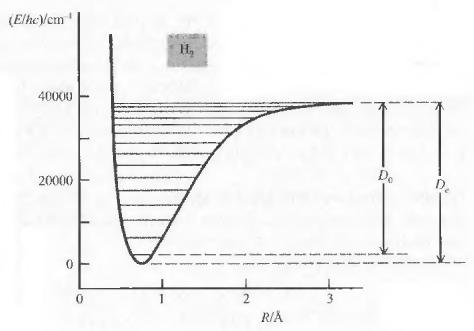
En el estado fundamental la energía rotacional es nula $(J=0, E_{rot}=0)$. Sin embargo, la energía vibracional en el estado fundamental de la molécula no es cero, con v=0 $E_{vib}=\frac{1}{2}h\nu_e -\frac{1}{4}h\nu_e x_e$. Obsérvese que se ha incluido la corrección de anarmonicidad.
Llamando $D_0$ a la energía de disociación del estado vibracional fundamental y $D_e$ energía de disociación de equilibrio, se puede escribir la siguiente relación entre ambas:
\begin{equation} D_e=D_0+\frac{1}{2}h\nu_e-\frac{1}{4}h\nu_ex_e \end{equation}
- Detalles
- Escrito por: Germán Fernández
- Categoría: Rotación vibración en moléculas diatómicas
- Visto: 1817
Al aumentar el número cuántico vibracional aumenta la energía vibracional de la molécula y también la distancia media entre los nucleos. El aumento de $R_{med}$ produce un incremento en el momento de inercia $I=\mu R_{med}^{2}$. La energía rotacional disminuye al ser inversamente proporcional al momento de inercia. Para considerar este efecto se añade a la energía el término $-h\alpha_e(v+1/2)J(J+1)$, siendo $\alpha_e$ la constante de acoplamiento rotación-vibración.
- Detalles
- Escrito por: Germán Fernández
- Categoría: Rotación vibración en moléculas diatómicas
- Visto: 2357
El aumentar la energía rotacional la distancia internuclear aumenta, debido a la fuerza centrífuga, que produce una aumento del momento de inercia. Esta distorsión hace que la energía rotacional sea inferior a la del rotor rígido y es necesario añadir la corrección $-hDJ^2(J+1)^2$, donde la constante de distorsión centrífuga D es una constante positiva pequeña.
- Detalles
- Escrito por: Germán Fernández
- Categoría: Rotación vibración en moléculas diatómicas
- Visto: 1858
La energía de una molécula diatómica con la inclusión de los términos de anarmonicidad, interacción rotación-vibración y distorsión centrífuga nos da
\begin{equation} E_{int}=E_{el}+h\nu_e(v+1/2)-h\nu_e x_e(v+1/2)^2+hB_eJ(J+1)-h\alpha_e(v+1/2)J(J+1)-hDJ^2(J+1)^2 \end{equation}
Si a esta energía interna le sumamos la energía traslacional obtenemos la energía total de la molécula $E=E_{tr}+E_{int}$



