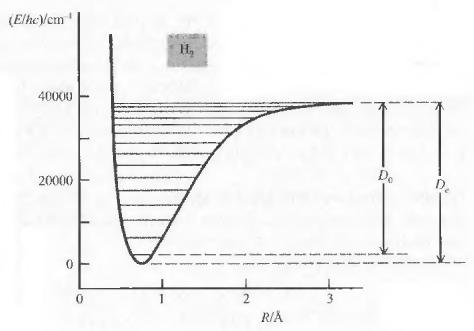
En el estado fundamental la energía rotacional es nula $(J=0, E_{rot}=0)$. Sin embargo, la energía vibracional en el estado fundamental de la molécula no es cero, con v=0 $E_{vib}=\frac{1}{2}h\nu_e -\frac{1}{4}h\nu_e x_e$. Obsérvese que se ha incluido la corrección de anarmonicidad.
Llamando $D_0$ a la energía de disociación del estado vibracional fundamental y $D_e$ energía de disociación de equilibrio, se puede escribir la siguiente relación entre ambas:
\begin{equation} D_e=D_0+\frac{1}{2}h\nu_e-\frac{1}{4}h\nu_ex_e \end{equation}
Cuestión: Calcular $D_o$ para el estado electrónico fundamental del $^{14}N$. Datos: $\frac{D_e}{hc}=79,89\;cm^{-1}$; $\bar{\nu}_e=2358,6\;cm^{-1}$; $\bar{\nu}_ex_e=14,3\;cm^{-1}$}
Solución: $\frac{D_o}{hc}=78714\;cm^{-1}$; $D_o=1,56\times 10^{-18}\;J$
Cuestión: (a) Explique por qué $D_e$ y $k_e$ para el $D^{35}Cl$ son esencialmente los mismos que $D_e$ y $k_e$ para $H^{35}Cl$, pero $D_o$ para estas dos especies son diferentes. (b) Calcular $D_o$ para estas dos especies, suponiendo que ambas tienen la misma constante de anarmonicidad $\bar{\nu}_ex_e$. Datos: $H^{35}Cl \rightarrow D_e/hc=37240\;cm^{-1}; \bar{\nu}_e=2990,9\;cm^{-1}; \bar{\nu}_ex_e=52,8\;cm^{-1}$.}
Solución: $D_o(H^{35}Cl)=7,103\times 10^{-19}\;J; D_o(D^{35}Cl)=7,187\times 10^{-19}\;J$



