In the ground state the rotational energy is zero $(J=0, E_{rot}=0)$. However, the vibrational energy in the ground state of the molecule is not zero, with v=0 $E_{vib}=\frac{1}{2}h\nu_e -\frac{1}{4}h\nu_e x_e$. Note that the anharmonicity correction has been included.
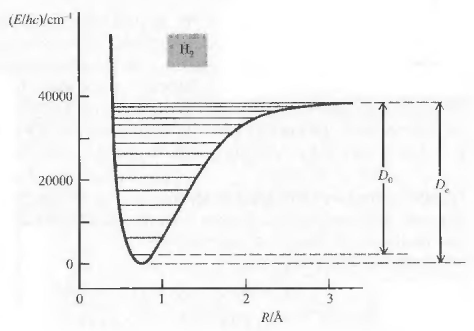
Calling $D_0$ the dissociation energy of the fundamental vibrational state and $D_e$ equilibrium dissociation energy, the following relation between the two can be written:
\begin{equation} D_e=D_0+\frac{1}{2}h\nu_e-\frac{1}{4}h\nu_ex_e \end{equation}
Question: Calculate $D_o$ for the fundamental electronic state of $^{14}N$. Data: $\frac{D_e}{hc}=79.89\;cm^{-1}$; $\bar{\nu}_e=2358.6\;cm^{-1}$; $\bar{\nu}_ex_e=14.3\;cm^{-1}$}
Solution: $\frac{D_o}{hc}=78714\;cm^{-1}$; $D_o=1.56\times 10^{-18}\;J$
Question: (a) Explain why $D_e$ and $k_e$ for $D^{35}Cl$ are essentially the same as $D_e$ and $k_e$ for $H^{35}Cl$, but $D_o $ for these two species are different. (b) Calculate $D_o$ for these two species, assuming that both have the same anharmonicity constant $\bar{\nu}_ex_e$. Data: $H^{35}Cl \rightarrow D_e/hc=37240\;cm^{-1}; \bar{\nu}_e=2990.9\;cm^{-1}; \bar{\nu}_ex_e=52.8\;cm^{-1}$.}
Solution: $D_o(H^{35}Cl)=7.103\times 10^{-19}\;J; D_o(D^{35}Cl)=7.187\times 10^{-19}\;J$



