Existen reacciones en las que la concentración de un reactante aumenta y disminuye con el tiempo de forma periódica. Este tipo de comportamiento está asociado a etapas autocatalíticas. En 1920 A. J. Lotka propuso un sencillo mecanismo en el que las concentraciones de los componentes X e Y oscilan periódicamente. El mecanismo de Lotka es el siguiente: \begin{equation} A+X\stackrel{k_1}{\rightarrow} 2X \end{equation} \begin{equation} X+Y\stackrel{k_2}{\rightarrow} 2Y \end{equation} \begin{equation} Y\stackrel{k_3}{\rightarrow} B \end{equation} El comportamiento oscilante de este sistema se observa si la concentración de A se mantiene constante, por tanto, es necesario añadir A al mismo ritmo que se gasta.
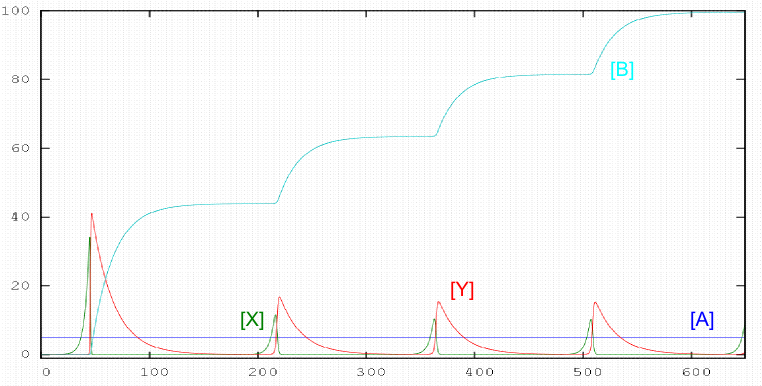
Uno de los sistemas más estudiados es el oregonator, propuesto por Field y Noyes en 1974. El mecanismo consta de 5 etapas: \begin{equation} A+Y\stackrel{k_1}{\rightarrow} X \end{equation} \begin{equation} X+Y\stackrel{k_2}{\rightarrow} P \end{equation} \begin{equation} B+X\stackrel{k_3}{\rightarrow}2X+Z \end{equation} \begin{equation} 2X\stackrel{k_4}{\rightarrow}Q \end{equation} \begin{equation} Z\stackrel{k_5}{\rightarrow}Y \end{equation} Estas 5 etapas se combinan en proporción {1,1,2,1,2} para dar la reacción global: $A+2B\rightarrow P+Q$ La gráfica se obtuvo para los siguientes valores de constantes cinéticas y concentraciones iniciales: \\ $k = \left(2.1, 2\times 10^9, 10^4, 4\times 10^7, 1\right)$\\ $\left([A], [B], [X], [Y], [Z], [P], [Q]\right) = \left(1, 1, 0, 0, 0.1, 0, 0 \right)$



